题目内容
1.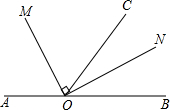 如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90°
如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90°(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由.
分析 (1)根据角的平分线的定义求得∠AOM的度数,然后根据邻补角的定义求得∠BOM的度数;
(2)首先根据∠MON=90°,∠AOB=180°,得出∠MOC+∠CON=90°,∠AOM+∠BON=90°,又∠AOM=∠MOC,根据等角的余角相等即可得到ON是∠BOC的角平分线.
解答 解:(1)∵OM平分∠AOC,
∴∠AOM=$\frac{1}{2}$∠AOC=55°,
∴∠BOM=∠AOB-∠AOM=180°-55°=125°;
(2)ON是∠BOC的角平分线.理由如下:
∵∠MON=90°,∠AOB=180°,
∴∠MOC+∠CON=90°,∠AOM+∠BON=90°,
又由(1)可知∠AOM=∠MOC,
∴∠CON=∠BON,
即ON是∠BOC的角平分线.
点评 本题考查了角度的计算,理解角平分线的定义以及互余的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
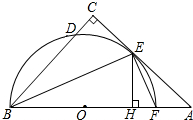 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.

 如图,在Rt△ABC中,∠C=90°,AC>BC,请用尺规作图方法把它分成两个三角形,且其中至少有一个是等腰三角形(保留作图痕迹,不写作法)
如图,在Rt△ABC中,∠C=90°,AC>BC,请用尺规作图方法把它分成两个三角形,且其中至少有一个是等腰三角形(保留作图痕迹,不写作法)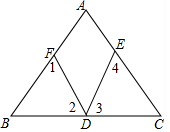 如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.
如图,D为BC上一点,∠1=∠2,∠3=∠4,∠A=50°,求∠EDF的度数.