题目内容
13．
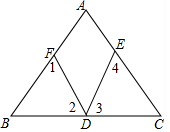如图，D为BC上一点，∠1=∠2，∠3=∠4，∠A=50°，求∠EDF的度数．
分析 根据三角形内角和定理求出∠B+∠C，根据三角形内角和定理得出∠1+∠2+∠B=180°，∠3+∠4+∠C=180°，求出∠2+∠3=115°，即可求出答案．
解答 解：∵∠A=50°，
∴∠B+∠C=180°-∠A=130°，
∵∠1+∠2+∠B=180°，∠3+∠4+∠C=180°，∠1=∠2，∠3=∠4，
∴2∠2+2∠3=360°-（∠B+∠C）=230°，
∴∠2+∠3=115°，
∴∠EDF=180°-（∠2+∠3）=65°．
点评 本题考查了三角形内角和定理，能灵活运用定理求出角的度数是解此题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
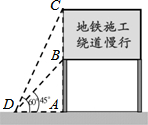某市备受关注的地铁六号线正紧张施工，为了缓解一些施工路段交通拥挤的现状，交警队设立了如图所示的交通略况显示牌，已知立杆AB的高度是3m，从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°，求路况显示牌BC的高度．
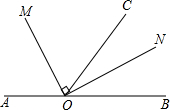如图，点O为直线AB上一点，∠AOC=110°，OM平分∠AOC，∠MON=90°
8．使（x2+px+8）（x2-3x+q）乘积中不含x2和x3项的p，q的值分别是（ ）
| A． | p=3，q=1 | B． | p=-3，q=-9 | C． | p=0，q=0 | D． | p=-3，q=1 |
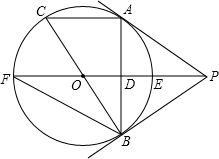如图，PA为⊙O的切线，A为切点，直线PO交⊙O与点E，F，过点A作PO的垂线AB，垂足为D，交⊙O与点B，延长BO与⊙O交与点C，连接AC，BF．
2．△ABC中，∠C=90°，sinA=$\frac{{2\sqrt{2}}}{3}$，则tanA的值是（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$ |
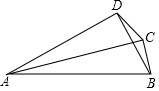如图，在四边形ABCD中，∠ACB=∠ADB=90°，且AC平分∠BAD．