题目内容
11．等边△ABC外有一点P，设P到三边的距离分别为h1，h2，h3，且h1-h2+h3=6，则△ABC的面积为12$\sqrt{3}$．分析 根据等边三角形的面积即可计算（h1-h2+h3）是等边三角形ABC的高，根据等边三角形的高即可求得BC的值，即可求得△ABC的面积，即可解题．
解答 
解：设等边△ABC的边长为a，连接PA、PB、PC，
则S△PAB+S△PBC-S△PAC=S△ABC，
从而$\frac{1}{2}$ah1-$\frac{1}{2}$ah2+$\frac{1}{2}$ah3=$\frac{\sqrt{3}}{4}$a2，
即 $\frac{1}{2}$a（h1-h2+h3）=$\frac{\sqrt{3}}{4}$a2，
∵h1-h2+h3=6，
∴a=4$\sqrt{3}$，
∴S△ABC=$\frac{\sqrt{3}}{4}$a2=12$\sqrt{3}$．
故答案为12$\sqrt{3}$．
点评 本题主要考查了等边三角形面积的计算，等边三角形高线长与边长的关系，本题中根据等边三角形的高计算等边三角形的面积是解题的关键．
练习册系列答案
相关题目
1．甲仓库有水泥100吨，乙仓库有水泥80吨，要全部运到A、B两工地，已知A工地需要70吨，B工地需要110吨，甲仓库运到A、B两工地的运费分别是140元/吨、150元/吨，乙仓库运到A、B两工地的运费分别是200元/吨、80元/吨，本次运动水泥总运费需要25900元．（运费：元/吨，表示运送每吨水泥所需的人民币）
（1）设甲仓库运到A工地水泥为x吨，请在下面表格中用x表示出其它未知量．
（2）用含x的代数式表示运送甲仓库100吨水泥的运费为-10x+15000元．（写出化简后的结果）
（3）求甲仓库运到A工地水泥的吨数．
（1）设甲仓库运到A工地水泥为x吨，请在下面表格中用x表示出其它未知量．
| 甲仓库 | 乙仓库 | |
| A工地 | x | 70-x |
| B工地 | 100-x | x+10 |
（3）求甲仓库运到A工地水泥的吨数．
如图，在△ABC中，∠B=90°，∠A=60°，AB=1，作等腰三角形△ACD，使∠CAD=30°，且点D和B位于AC异侧，连结BD交AC于点O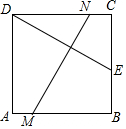
如图，将边长为8厘米的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段MN的长是4$\sqrt{5}$cm．
已知，如图，在Rt△ABC中，AC=6，BC=8，D边AB上一点，连接CD，过点D作DE⊥DC交BC于E，把△BDE沿DE翻折得△DEB1，连接B1C．
如图，抛物线y=-x2+20的图象与y轴正半轴的交点为A，将线段OA分成20等份，设分点分别为P1，P2，…，P19，过每个分点作y轴的垂线，分别与抛物线交于点Q1，Q2，…，记△OP1Q1，△P1P2Q2，…的面积分别为S1，S2，…，S19，则S12+S22+…+S192的值为（ ）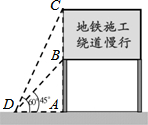
某市备受关注的地铁六号线正紧张施工，为了缓解一些施工路段交通拥挤的现状，交警队设立了如图所示的交通略况显示牌，已知立杆AB的高度是3m，从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°，求路况显示牌BC的高度．
如图所示，以O为端点画六条射线：OA，OB，OC，OD，OE，OF，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，…，那么按图中规律，所描的第59个点在射线OE上，第2017个点在射线OA上．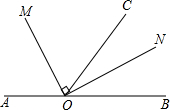
如图，点O为直线AB上一点，∠AOC=110°，OM平分∠AOC，∠MON=90°