题目内容
8．
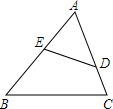如图，D、E分别是AC、AB上的点，△ADE∽△ABC，且DE=4，BC=12，CD=9，AD=3，求AE、BE的长．
分析 由△ADE∽△ABC，且DE=4，BC=12，CD=9，AD=3，根据相似三角形的对应边成比例，即可求得答案．
解答 解：∵△ADE∽△ABC，
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{DE}{BC}$，
∵DE=4，BC=12，CD=9，AD=3，
∴AC=ADD+CD=12，
∴AE=4，AB=9，
∴BE=AB-AE=5．
点评 此题考查了相似三角形的性质．注意掌握相似三角形的对应边成比例定理的应用是解此题的关键．
练习册系列答案
相关题目
如图所示，在一次“寻宝”游戏中，已知寻宝图上两个标志点A（-3，0）和点B（5，0），宝藏分别埋在C（3，4）和D（-2，3）两点．请你首先建立直角坐标系确定宝藏的位置，然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积．
如图一个圆桶，底面直径为6cm，高为12cm，则沿桶的侧面从点A到点B的最短距离为$\sqrt{9π+144}$．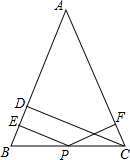
如图，在△ABC中，AB=AC，CD⊥AB于D，P为BC上的任意一点，过P点分别作PE⊥AB，PF⊥CA，垂足分别为E，F，则有PE+PF=CD，你能说明为什么吗？