题目内容
13．
如图一个圆桶，底面直径为6cm，高为12cm，则沿桶的侧面从点A到点B的最短距离为$\sqrt{9π+144}$．
分析 先将圆柱的侧面展开为一矩形，而矩形的长就是底面周长的一半，高就是圆柱的高，再根据勾股定理就可以求出其值．
解答 
解：展开圆柱的侧面如图，根据两点之间线段最短就可以得知AB最短．由题意，得
AC=3π，在Rt△ABC中，由勾股定理，得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{9π+144}$cm．
故答案为：$\sqrt{9π+144}$cm．
点评 本题考查了圆柱侧面展开图的运用，两点之间线段最短的运用，勾股定理的运用．在解答时将圆柱的侧面展开是关键．
练习册系列答案
相关题目
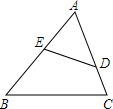如图，D、E分别是AC、AB上的点，△ADE∽△ABC，且DE=4，BC=12，CD=9，AD=3，求AE、BE的长．