题目内容
17.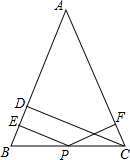 如图,在△ABC中,AB=AC,CD⊥AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F,则有PE+PF=CD,你能说明为什么吗?
如图,在△ABC中,AB=AC,CD⊥AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F,则有PE+PF=CD,你能说明为什么吗?
分析 在CG上截取CH=PE,连接H,易证四边形GEPH是矩形,从而可知∠GHD=90°,PH∥AB,那么就有∠PHC=∠CFP=90°,∠HPC=∠B,又AB=AC,利用等边对等角,可得∠B=∠FCP,于是∠HPC=∠FCP,再结合CP=PC,利用AAS可证△PHC≌△CFP,那么CH=PF,从而易证PE+PF=CG.
解答  证明:如图所示,在CD上截取DH=EP,并连接HP,
证明:如图所示,在CD上截取DH=EP,并连接HP,
∵CD⊥AB,PE⊥AB,
∴PE∥CD,PH∥ED,∠HDE=90°,
∴四边形PHDE是矩形,
∴∠PHD=90°,
∴∠PHC=90°,
在△PHC和△CFP中,
∠PHC=∠CFP=90°,
∵PH∥AB,AB=AC,
∴∠HPC=∠B=∠FCP,
在△PHC与△CFP中,$\left\{\begin{array}{l}{∠HPC=∠FCP}\\{∠PHC=∠CFP}\\{PC=PC}\end{array}\right.$,
∴△PHC≌△CFP,
∴HC=FP,
∴PE+PF=DH+HC=CD,
即PE+PF=CD.
点评 本题考查了全等三角形的判定与性质及等腰三角形的性质;辅助线的作出是正确解答本题的关键.

练习册系列答案
相关题目
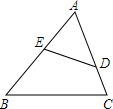 如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长. 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论: