题目内容
6.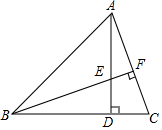 如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.
如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.(1)求证:AD=BD;
(2)若∠C=65°,求∠ABE的度数.
分析 (1)利用同角的余角相等求出∠C=∠BED,再利用“角角边”证明△ACD和△BED全等,根据全等三角形对应边相等证明即可;
(2)根据直角三角形两锐角互余求出∠FBC,再求出△ABD是等腰直角三角形,根据等腰直角三角形的性质求出∠ABD=45°,再根据∠ABE=∠ABD-∠CBF代入数据计算即可得解.
解答 (1)证明:∵AD是△ABC一边上的高,BF⊥AC,
∴∠C+∠CBE=90°,
∠BED+∠CBE=90°,
∴∠C=∠BED,
在△ACD和△BED中,$\left\{\begin{array}{l}{∠C=∠BED}\\{∠ADC=∠BDE=90°}\\{BE=AC}\end{array}\right.$,
∴△ACD≌△BED(AAS),
∴AD=BD;
(2)解:∵BF⊥AC,
∴∠CBF=90°-∠C=90°-65°=25°,
∵AD⊥BC,AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABD=45°,
∴∠ABE=∠ABD-∠CBF=45°-25°=20°.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,同角的余角相等的性质,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
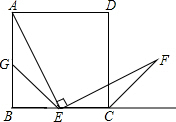 如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.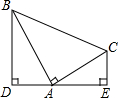 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,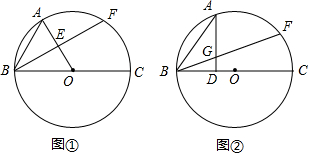
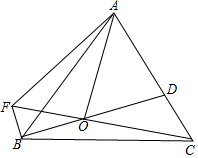 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$. 已知:如图,P、Q是△ABC边BC上两点,且AB=AC,AP=AQ.求证:BP=CQ.
已知:如图,P、Q是△ABC边BC上两点,且AB=AC,AP=AQ.求证:BP=CQ.