题目内容
1.某商场经营某种品牌的童装,购进时的单价是50元.根据市场调查,在一段时间内,销售单价是80元时,销售量是280件.而销售单价每降低1元,就可多售出20件.(1)求出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;
(2)若童装厂规定该品牌童装销售单价不低于75元,且商场要完成不少于340件的销售
任务,则商场销售该品牌童装获得的最大利润是多少元?
(3)如果要使利润不低于6800元,那么销售单价应在什么取值范围内?
分析 (1)利润w等于单件利润×销售量,即W=(x-50)[280+(80-x)×20]整理即可;
(2)利用x的取值范围结合二次函数增减性,进而得出最大利润;
(3)根据利润不低于6800元可得-20x2+2880x-94000≥6800,解之可得x的范围;
解答 解:(1)w=(x-50)[280+(80-x)×20]
=(x-50)(1880-20x)
=-20x2+2880x-94000;
(2)由题意,得$\left\{\begin{array}{l}{x≥75}\\{280+20(80-x)≥340}\end{array}\right.$,
解得:75≤x≤77,
由①w=-20x2+2880x-94000,
∵x=-$\frac{b}{2a}$=72,-20<0,
∴当x>72时,w随x增大而减少.
又∵75≤x≤77,
∴当x=75时,w最大=-20×752+2880×75-94000=9500(元),
答:该商场销售该品牌童装获得的最大利润是9500元;
(3)根据题意可得-20x2+2880x-94000≥6800,
解得:60≤x≤84,
又∵50≤x≤80,
∴60≤x≤80,
答:要使利润不低于6800元,那么销售单价应满足60≤x≤80.
点评 本题主要考查二次函数的应用,理解题意找到题目蕴含的相等关系或不等关系是列函数解析式和不等式的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 已知:如图,AB=CD,AD=BC,求证:∠A=∠C.
已知:如图,AB=CD,AD=BC,求证:∠A=∠C. 已知:如图,AD=BC,AB=DC,求证:∠A=∠C.
已知:如图,AD=BC,AB=DC,求证:∠A=∠C.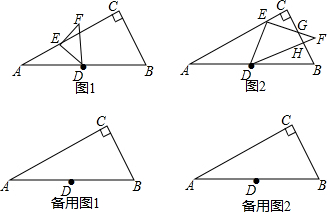
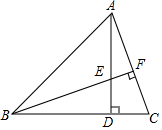 如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.
如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.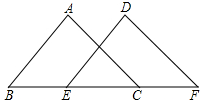 如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,∠A=∠D,AB∥DE,BE=CF,求证:AC∥DF.