题目内容
14.如图所示,BC是圆O的直径,点A、F在圆O上,连接AB、BF.(1)如图1,若点A、F把半圆三等分,连接OA,OA与BF交于点E.求证:E为OA的中点;
(2)如图2,若点A为弧$\widehat{BF}$的中点,过点A作AD⊥BC,垂足为点D,AD与BF交于点G.求证:AG=BG.
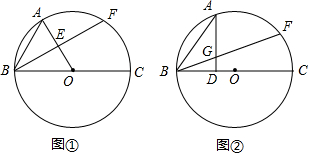
分析 (1)先求出∠AOB的度数,故可判断出△OAB为等边三角形,再由A为弧BF中点可得出OA⊥BF,进而可得出结论;
(2)连接AF,AC,根据弧相等可得出∠C=∠ABF,由圆周角定理可得出∠BAC=90°,再由直角三角形的性质得出∠ABG=∠BAG,进而可得出结论.
解答 证明:(1)∵A、F为半圆三等分点,
∴∠AOB=$\frac{1}{3}$×180°=60°,
∵OA=OB,
∴△OAB为等边三角形.
∵A为弧BF中点,
∴OA⊥BF,
∴BE平分OA,
∴E为OA中点.
(2)连接AF,AC,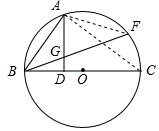
∵A为弧BF中点,
∴$\widehat{AB}$=$\widehat{AF}$,
∴∠ABF=∠F.
∵$\widehat{AB}$=$\widehat{AB}$,
∴∠C=∠F,
∴∠C=∠ABF.
∵BC为圆O的直径,
∴∠BAC=90°,
∴∠BAD+∠CAD=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠ABG=∠BAG,
∴AG=BG.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
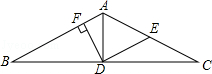 如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证:
如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证: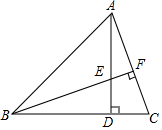 如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.
如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.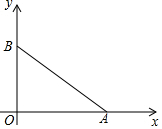 如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.
如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.