题目内容
12.计算:$\frac{1}{2}$$\sqrt{18}$+(π+1)0-sin45°+|$\sqrt{2}$-2|分析 原式利用二次根式性质,零指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果.
解答 解:原式=$\frac{1}{2}$×3$\sqrt{2}$+1-$\frac{\sqrt{2}}{2}$+2-$\sqrt{2}$
=3.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.已知一个正多边形的内角是140°,则这个正多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
7.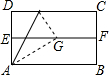 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
4.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数是( )


| A. | 2n+1 | B. | n2-1 | C. | n2+2n | D. | 5n-2 |
8.已知4<a<7,$\sqrt{(a-4)^{2}}+\sqrt{(a-7)^{2}}$化简后为( )
| A. | 3 | B. | -3 | C. | 2a-11 | D. | 11-2a |
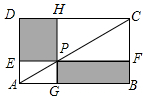 如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.