题目内容
一圆的半径是10cm,圆内的两条平行弦长分别为12cm和16cm,则这两条平行弦之间的距离为 .
考点:垂径定理,平行线的性质,勾股定理
专题:分类讨论
分析:过O作MN⊥AB于M,交CD于N,连接OB,OD,有两种情况:①当AB和CD在O的两旁时,根据垂径定理求出BM,DN,根据勾股定理求出OM,ON,相加即可;②当AB和CD在O的同旁时,ON-OM即可.
解答: 解:有两种情况:①如图,当AB和CD在O的两旁时,
解:有两种情况:①如图,当AB和CD在O的两旁时,
过O作MN⊥AB于M,交CD于N,连接OB,OD,
∵AB∥CD,
∴MN⊥CD,
由垂径定理得:BM=
AB=8cm,DN=
CD=6cm,
∵OB=OD=10cm,
由勾股定理得:OM=
=6cm,
同理ON=8cm,
∴MN=8cm+6cm=14cm,
②当AB和CD在O的同旁时,MN=8cm-6cm=2cm,
故答案为:14cm或2cm.
 解:有两种情况:①如图,当AB和CD在O的两旁时,
解:有两种情况:①如图,当AB和CD在O的两旁时,过O作MN⊥AB于M,交CD于N,连接OB,OD,
∵AB∥CD,
∴MN⊥CD,
由垂径定理得:BM=
| 1 |
| 2 |
| 1 |
| 2 |
∵OB=OD=10cm,

由勾股定理得:OM=
| OB2-BM2 |
同理ON=8cm,
∴MN=8cm+6cm=14cm,
②当AB和CD在O的同旁时,MN=8cm-6cm=2cm,
故答案为:14cm或2cm.
点评:本题考查了垂径定理和勾股定理的应用,关键是理解题意,能得出两种情况,题目比较典型,难度适中.注意要进行分类讨论.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,则tanA•tanB等于( )
| A、0 | B、1 | C、-1 | D、不确定 |
若a,b是一元二次方程x2+2x-1=0的两根,则下列说法正确的是( )
| A、a+b=2 |
| B、a+b=-1 |
| C、ab=-1 |
| D、ab=1 |
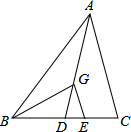 如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.
如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD. 在△ABC中,点D、E分别在AB、AC边上,连结DE,要使△ADE与△ABC相似,应添加的条件是
在△ABC中,点D、E分别在AB、AC边上,连结DE,要使△ADE与△ABC相似,应添加的条件是 如图,已知AB=AC,BD⊥AC于点D,求证:∠DBC=
如图,已知AB=AC,BD⊥AC于点D,求证:∠DBC=