题目内容
11.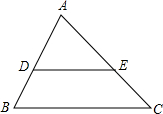 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
分析 由DE∥BC,根据平行线的性质可得出∠C=∠AED,再根据三角形的内角和为180°结合给定条件即可得出结论.
解答 解:∵DE∥BC,
∴∠C=∠AED=40°.
又∵∠A+∠B+∠C=180°,∠B=60°,
∴∠A=80°.
故选B.
点评 本题考查了平行线的性质以及三角形内角和定理,解题的关键是找出∠C=∠AED.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
相关题目
2.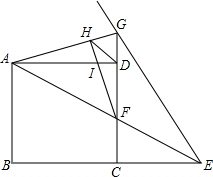 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
①GE+GD=BE;②DG=DF;③AC-2HD=$\sqrt{2}$DF;④当CE=BC=2时,FG=$\frac{5}{3}$.
 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )①GE+GD=BE;②DG=DF;③AC-2HD=$\sqrt{2}$DF;④当CE=BC=2时,FG=$\frac{5}{3}$.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
6.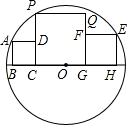 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
2.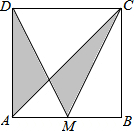 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
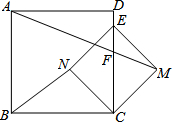 如图,在正方形ABCD中,E为CD边上一点,以CE为对角线构造正方形CMEN,点N在正方形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为$\frac{25}{7}$.
如图,在正方形ABCD中,E为CD边上一点,以CE为对角线构造正方形CMEN,点N在正方形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为$\frac{25}{7}$.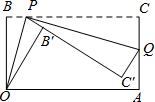 已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为
已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为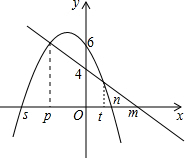 如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0). 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.