题目内容

11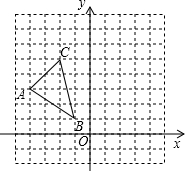．在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系，并给出了格点△ABC（顶点是网格线的交点）．
（1）画出△ABC绕坐标原点O顺时针旋转90°得到的格点△A1B1C1；
（2）直接写出点A在旋转变换过程中所经过的路径长（不用说理）．

分析 （1）利用网格特点和旋转的性质画出点A、B、C的对应点A1、B1、C1，即可得到△A1B1C1；
（2）点A在旋转变换过程中所经过的路径是以O点为圆心，OA为半径，圆心角为90度的弧，然后根据弧长公式计算点A在旋转变换过程中所经过的路径长即可．

解答 解：（1）如图，点△A1B1C1为所作；

（2）点A在旋转变换过程中所经过的路径长=$\frac{90•π•5}{180}$=$\frac{5}{2}$π．

点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．

练习册系列答案
相关题目
1．若x1、x2是关于x的一元二次方程ax2+bx+c=0（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$，我们把它们称为根与系数的关系定理，请你参考上述定理，解答下列问题：
设二次函数y=ax2+bx+c（a≠0）的图象与x轴的两个交点为A（x1，0），B（x2，0）．抛物线的顶点为C，且△ABC为等腰三角形．
（1）求A、B两点之间的距离（用字母a、b、c表示）
（2）当△ABC为等腰直角三角形时，求b2-4ac的值；
（3）设抛物线y=x2+kx+1与x轴的两个交点为A、B，顶点为C，且∠ACB=90°，试问如何平移此抛物线，才能使∠ACB=60°？
2．如图，一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B，与反比例函数y=$\frac{k}{x}$（k≠0）的图象的一个交点为A（2，m）．
（1）求反比例函数的表达式；
（2）过点A作AC⊥x轴，垂足为点C，设点D在反比例函数图象上，且△DBC的面积等于6，请求出点D的坐标；
（3）请直接写出不等式$\frac{1}{2}$x+2＜$\frac{k}{x}$成立的x取值范围．
19．（1）求不等式组$\left\{\begin{array}{l}{x+3≥\frac{1}{2}x}\\{5-2x＜9}\end{array}\right.$的解集；
（2）如图，在△ABC中，己知∠ABC=30°，将△ABC绕点B逆时针旋转50°后得到△A′BC′，已知A′C′∥BC，求∠A的度数．
6．将矩形ABCD的一边AB沿AE对折，使AB沿AE对折，使AB落在边AD上，点B与点F重合，求证：四边形ABEF是正方形．
16．以下列数组为边长的三角形，恰好是直角三角形的是（　　）
A．4，6，8B．4，8，10C．6，8，10D．8，10，12
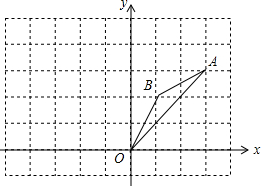3．如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，3），B（1，2），△AOB绕点O逆时针旋转90°后得到△A1OB1．
（1）画出△A1OB1，直接写出点B1关于点O的对称点B2的坐标；
（2）请直接写出：以A、B、O、C为顶点的平行四边形的第四个顶点C的坐标；
（3）请直接写出：在旋转过程中，点B经过的路径的长；
（4）求在旋转过程中，线段AB所扫过的面积．
20．已知平行四边形ABCD中，∠A比∠B大40°，则∠BCD的度数为110°．
1．如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=1，∠B=60°，则△ACD的面积为（　　）
A．2$\sqrt{3}$B．$\sqrt{3}$C．$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网