题目内容
1.若x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,我们把它们称为根与系数的关系定理,请你参考上述定理,解答下列问题:设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).抛物线的顶点为C,且△ABC为等腰三角形.
(1)求A、B两点之间的距离(用字母a、b、c表示)
(2)当△ABC为等腰直角三角形时,求b2-4ac的值;
(3)设抛物线y=x2+kx+1与x轴的两个交点为A、B,顶点为C,且∠ACB=90°,试问如何平移此抛物线,才能使∠ACB=60°?
分析 (1)令二次函数解析式中y=0,根据根与系数的关系可得出“x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$”,利用配方法即可求出|x2-x1|的值,由此即可得出结论;
(2)利用配方法将二次函数解析式转化成顶点式,由此即可求出点C的坐标,再根据等腰直角三角形的性质可得出2×|$\frac{4ac-{b}^{2}}{4a}$|=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$,利用换元解方程即可求出b2-4ac的值;
(3)由(2)的结论即可得出关于k的方程,解方程即可得出抛物线的解析式,画出函数图象,由此可得出若要使∠ACB=60°,则需把抛物线往下平移,设平移的距离为n(n>0),则平移后的抛物线的解析式为y=x2-2$\sqrt{2}$x+1-n,结合(1)(2)的结论即可得出关于n的一元二次方程,解方程即可得出结论.
解答 解:(1)令y=ax2+bx+c(a≠0)中y=0,则有ax2+bx+c=0,
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0),
∴x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,
∴|x2-x1|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(-\frac{b}{a})^{2}-4×\frac{c}{a}}$=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$.
(2)∵二次函数y=ax2+bx+c=a$(x+\frac{b}{2a})^{2}$+$\frac{4ac-{b}^{2}}{4a}$,
∴点C的坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
∵△ABC为等腰直角三角形,
∴2×|$\frac{4ac-{b}^{2}}{4a}$|=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$,
令$\sqrt{{b}^{2}-4ac}$=m,则有m2-2m=0,
解得:m=2,或m=0,
∵二次函数与x轴有两个不相同的交点,
∴m=$\sqrt{{b}^{2}-4ac}$=2,
∴b2-4ac=4.
(3)∵∠ACB=90°,
∴b2-4ac=k2-4=4,
解得:k=±2$\sqrt{2}$.
选k=-2$\sqrt{2}$,画出图形,如图所示.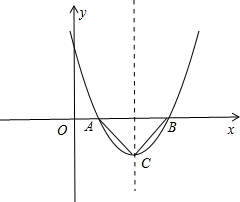
若要使∠ACB=60°,则需把抛物线往下平移,设平移的距离为n(n>0),则平移后的抛物线的解析式为y=x2-2$\sqrt{2}$x+1-n,
由(1)可知AB=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$=2$\sqrt{1+n}$,
由(2)可知点C(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),即($\sqrt{2}$,-1-n),
∵△ABC为等腰三角形,且∠ACB=60°,
∴-yC=$\frac{\sqrt{3}}{2}$AB,即1+n=$\sqrt{3}$$\sqrt{1+n}$,
解得:n=-1(舍去),或n=2.
故将抛物线往下平移2个单位长度,能使∠ACB=60°.
点评 本题考查了根与系数的关系、等腰直角三角形的性质、等边三角形的性质以及解一元二次方程,解题的关键是:(1)利用配方法求出|x2-x1|的值;(2)利用换元法解方程;(3)根据等边三角形的性质找出关于n的方程.本题属于中档题,难度不大,但解题过程稍显繁琐,解决该题型题目时,利用等腰直角(等边)三角形的性质得出边与边的关系是关键.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案 如图,直线AB和CD相交于点O,若∠AOD=134°,则∠AOC的度数为( )
如图,直线AB和CD相交于点O,若∠AOD=134°,则∠AOC的度数为( )| A. | 134° | B. | 144° | C. | 46° | D. | 32° |
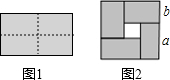 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )| A. | ab | B. | (a+b)2 | C. | (a-b)2 | D. | a2-b2 |
 四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,求DH的长.
四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,求DH的长. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC=1:2.
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC=1:2.
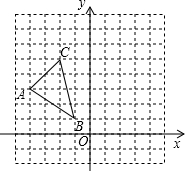 在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点是网格线的交点).
在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点是网格线的交点).