题目内容
6．
将矩形ABCD的一边AB沿AE对折，使AB沿AE对折，使AB落在边AD上，点B与点F重合，求证：四边形ABEF是正方形．
分析 根据正方形的性质和翻折变换的性质可知得到四边形ABEF是矩形，根据翻折变换的性质得到AB=AF，根据正方形的判定定理证明即可．
解答 解：正方形的性质和翻折变换的性质可知，∠B=∠BAF=∠AFE=90°，
∴四边形ABEF是矩形，
由翻折变换的性质可知，AB=AF，
∴四边形ABEF是正方形．
点评 本题考查的是翻折变换的性质、正方形的判定，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
名校课堂系列答案
相关题目
16．
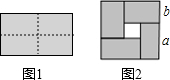如图1是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空的部分的面积为（ ）
如图1是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空的部分的面积为（ ）| A． | ab | B． | （a+b）2 | C． | （a-b）2 | D． | a2-b2 |
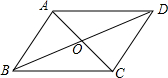如图，在?ABCD中，已知AC、BD相交于点O，两条对角线的和为24cm，BC长为8cm，则△AOD的周长=20cm．
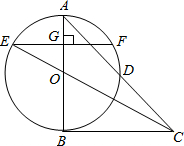如图，在△ABC中，∠A=45°，以AB为直径的⊙O交于AC的中点D，连接CO，CO的延长线交⊙O于点E，过点E作EF⊥AB，垂足为点G．
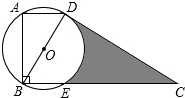如图，在四边形ABCD中，AD∥BC，∠ABC=90°，AD=$\sqrt{3}$，CD=6，以对角线BD为直径作⊙O与CD交于点D，与BC交于点E，且∠ABD为30°．
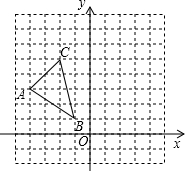在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系，并给出了格点△ABC（顶点是网格线的交点）．
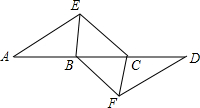如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．
如图，在三角形ABC中，BE平分∠ABC，DE∥BC，则图中相等的角有5对．