题目内容
6．
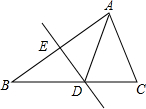如图所示．将△ABC沿直线DE折叠后，使点B与点A重合，已知AC=4cm，△ADC的周长为11cm，则BC的长为（ ）| A． | 11cm | B． | 15cm | C． | 7cm | D． | 10cm |
分析 利用翻折变换的性质得出AD=BD，进而利用AD+CD=BC得出即可．
解答 解：∵将△ABC沿直线DE折叠后，使得点B与点A重合，
∴AD=BD，
∵AC=4cm，△ADC的周长为15cm，
∴AD+CD=BC=11-4=7（cm）．
故选C．
点评 此题主要考查了翻折变换的性质，根据题意得出AD=BD是解题关键．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
16．
已知圆的半径是2$\sqrt{3}$，则该圆的内接正六边形的面积是（ ）
已知圆的半径是2$\sqrt{3}$，则该圆的内接正六边形的面积是（ ）| A． | 3$\sqrt{3}$ | B． | 9$\sqrt{3}$ | C． | 18$\sqrt{3}$ | D． | 36$\sqrt{3}$ |
17．下列运算正确的是（ ）
| A． | a6÷a=a6 | B． | （xy2）3=xy6 | C． | （$\frac{1}{2}$）-1=-2 | D． | 20160=1 |
1．若分式$\frac{|x|-2}{x+2}$的值为0，则x=（ ）
| A． | 2或-2 | B． | 2 | C． | -2 | D． | 以上都不对 |
（1）解方程：$\frac{x}{x-2}$=$\frac{2}{x-2}$-1