题目内容
20．若三角形的两边长分别是4和6，第三边的长是一元二次方程x2-7x+12=0的一个实数根，则该三角形的周长是（ ）| A． | 13 | B． | 14 | C． | 17 | D． | 13或14 |
分析 因式分解法求得x的值，再根据周长公式可得答案．
解答 解：∵（x-3）（x-4）=0，
∴x-3=0或x-4=0，
解得：x=3或x=4，
当x=3时，三角形的三边为3、4、6，其周长为3+4+6=13；
当x=4时，三角形三边为4、4、6，其周长为4+4+6=14；
故选：D．
点评 本题主要考查解一元二次方程的能力和三角形三边的关系，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
（1）解方程：$\frac{x}{x-2}$=$\frac{2}{x-2}$-1
8．
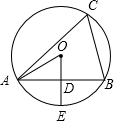如图⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，若⊙O的半径为2，则下列结论错误的是（ ）
如图⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，若⊙O的半径为2，则下列结论错误的是（ ）| A． | AD=BD | B． | AE=BE | C． | AB=$\sqrt{3}$ | D． | OD=1 |
