题目内容
3.已知:x2-4x+4与|y-1|互为相反数,则式子($\frac{y}{x}$-$\frac{x}{y}$)÷(x+y)的值等于-$\frac{1}{2}$.分析 根据相反数的性质得出x2-4x+4+|y-1|=0,根据非负数的性质得出x,y的值,代入计算即可.
解答 解:∵x2-4x+4与|y-1|互为相反数,
∴x2-4x+4+|y-1|=0,
∴(x-2)2+|y-1|=0,
∴x-2=0,y-1=0,
∴x=2,y=1,
∴原式=$\frac{{y}^{2}-{x}^{2}}{xy}$•$\frac{1}{x+y}$
=$\frac{y-x}{xy}$
=$\frac{-1}{2}$
=-$\frac{1}{2}$,
故答案为-$\frac{1}{2}$.
点评 本题考查了非负数的性质,掌握几个非负数的和为0,这几个数都等于0是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
8.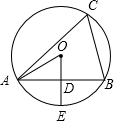 如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
 如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )| A. | AD=BD | B. | AE=BE | C. | AB=$\sqrt{3}$ | D. | OD=1 |
 (1)解方程:$\frac{x}{x-2}$=$\frac{2}{x-2}$-1
(1)解方程:$\frac{x}{x-2}$=$\frac{2}{x-2}$-1