题目内容
10.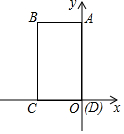 如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
分析 当AP=PD时,点P在AD的垂直平分线上,得到P(-6,4),当AP=AD=8时,当DP=AD=8时,根据勾股定理即可得到结论.
解答  解:如图,
解:如图,
当AP=PD时,
点P在AD的垂直平分线上,
∴P(-6,4),
当AP=AD=8时,
BP=$\sqrt{A{P}^{2}-A{B}^{2}}$=2$\sqrt{7}$,
当DP=AD=8时,
PC=2$\sqrt{7}$,
∴P(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$),
∴P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
故答案为:(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
点评 本题考查了等腰三角形的性质,坐标与图形性质,矩形的性质,正确的作出图形是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
20.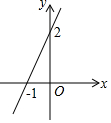 如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
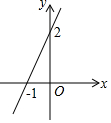 如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )
如图所示是一次函数y=kx+b在直角坐标系中的图象,通过观察图象我们就可以得到方程kx+b=0的解为x=-1,这一求解过程主要体现的数学思想是( )| A. | 数形结合 | B. | 分类讨论 | C. | 类比 | D. | 公理化 |
2.关于x的一元二次方程(m-1)x2+2x+m2-5m+4=0,常数项为0,则m值等于( )
| A. | 1 | B. | 4 | C. | 1或4 | D. | 0 |
19.我市某镇组织20辆汽车装运完A,B,C三种脐橙共100吨到外地销售,按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满,根据下表提供的信息,解答以下问题:
(1)设装运A种脐橙的车辆数为x,装运B种脐橙的车辆数为y,则装运C种脐橙的车辆数为(20-x-y)辆.(用含x,y式子表示),根据三种脐橙共100吨,可列得二元一次方程为6x+5y+4(20-x-y)=100.用含x的式子表示y为y=20-2x.
(2)如果装运每种脐橙的车辆数都不少于6辆,如果你是水果老板,请你写出运送方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
| 脐橙品种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨脐橙获得(百元) | 12 | 16 | 10 |
(2)如果装运每种脐橙的车辆数都不少于6辆,如果你是水果老板,请你写出运送方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
 如图,在四边形ABCD中,AB∥CD,AE平分∠BAD交BC于点E,且AB=EB.求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,AE平分∠BAD交BC于点E,且AB=EB.求证:四边形ABCD是平行四边形.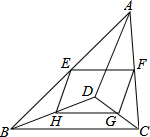 如图,D是△ABC内一点,AD=7,BC=5,若E、F、C、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是12.
如图,D是△ABC内一点,AD=7,BC=5,若E、F、C、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是12. 如图,在?ABCD中,∠BAD的平分线交DC于点E,若DE:EC=3:1,AB的长为8,AB边上的高线长为5,求BC与AD之间的距离.
如图,在?ABCD中,∠BAD的平分线交DC于点E,若DE:EC=3:1,AB的长为8,AB边上的高线长为5,求BC与AD之间的距离.