题目内容
1. 如图,在四边形ABCD中,AB∥CD,AE平分∠BAD交BC于点E,且AB=EB.求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,AE平分∠BAD交BC于点E,且AB=EB.求证:四边形ABCD是平行四边形.
分析 首先根据AE平分∠∠BAD交BC于点E得到∠DAE=∠BAE,然后根据AB=EB得到∠BAE=∠BEA,从而得到∠BEA=∠DAE,利用内错角相等两直线平行得到AD∥BC,然后根据AB∥CD利用两组对边分别平行的四边形是平行四边形证得结论即可.
解答 解:∵AE平分∠∠BAD交BC于点E,
∴∠DAE=∠BAE,
∵AB=EB,
∴∠BAE=∠BEA,
∴∠BEA=∠DAE,
∴AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形.
点评 本题考查了平行四边形的判定,了解平行四边形的判定定理是解答本题的关键,难度不大.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12.若$\sqrt{x-1}$+(y+2)4=0,则(x+y)2017等于( )
| A. | -1 | B. | 1 | C. | 32016 | D. | -32016 |
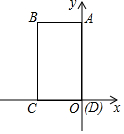 如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).