题目内容
19.我市某镇组织20辆汽车装运完A,B,C三种脐橙共100吨到外地销售,按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满,根据下表提供的信息,解答以下问题:| 脐橙品种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨脐橙获得(百元) | 12 | 16 | 10 |
(2)如果装运每种脐橙的车辆数都不少于6辆,如果你是水果老板,请你写出运送方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
分析 (1)设装运A种脐橙的车辆数为x,装运B种脐橙的车辆数为y,利用共有20辆车可表示出装运C种脐橙的车辆数为(20-x-y)辆,再利用三种脐橙共100吨,可列得二元一次方程为6x+5y+4(20-x-y)=100,然后用含x的式子表示y;
(2)利用装运每种脐橙的车辆数都不少于6辆可列三个不等式,然后解不等式组,再写出整数x的值即可得到方案;
(3)分别计算出(2)中各方案的利润,然后比较大小即可.
解答 解:(1)设装运A种脐橙的车辆数为x,装运B种脐橙的车辆数为y,则装运C种脐橙的车辆数为(20-x-y)辆,
根据三种脐橙共100吨,可列得二元一次方程为6x+5y+4(20-x-y)=100,用含x的式子表示y为y=20-2x;
故答案为(20-x-y)辆,6x+5y+4(20-x-y)=100,y=20-2x;
(2)根据题意得$\left\{\begin{array}{l}{x≥6}\\{y≥6}\\{20-x-y≥6}\end{array}\right.$,解得6≤x≤7,
所以x=6或7,
运送方案为:方案1:装运A种脐橙的车辆数为6,装运B种脐橙的车辆数为8,装运C种脐橙的车辆数为6;
方案2:装运A种脐橙的车辆数为7,装运B种脐橙的车辆数为6,装运C种脐橙的车辆数为7;
(3)方案1的费用为:6×6×12+8×5×16+6×4×10=1312(百元)
方案2的费用为:7×6×12+6×5×16+7×4×10=1264(百元),
所以安排装运A种脐橙的车辆数为6,装运B种脐橙的车辆数为8,装运C种脐橙的车辆数为6,销售获利最大,最大利润的值为1312百元.
点评 本题考查了一元一次不等式的应用:由实际问题中的不等关系列出不等式,建立解决问题的数学模型,通过解不等式可以得到实际问题的答案.列不等式解应用题需要以“至少”、“最多”、“不超过”、“不低于”等词来体现问题中的不等关系.因此,建立不等式要善于从“关键词”中挖掘其内涵.

| A. | (x-6)2=34 | B. | (x+6)2=34 | C. | (x-3)2=7 | D. | (x-3)2=11 |
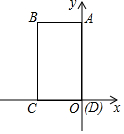 如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$). 如图.在?ABCD中,BE⊥DC于E,BF⊥DA于F,若∠A=30°,BE=6.BF=9.求?ABCD的面积和周长.
如图.在?ABCD中,BE⊥DC于E,BF⊥DA于F,若∠A=30°,BE=6.BF=9.求?ABCD的面积和周长.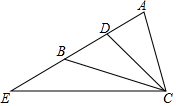 已知如图所示,在等腰△ABC中,AB=AC,CD是中线,延长AB到E,使得BE=AB,连结CE,求证:CD=$\frac{1}{2}$CE.
已知如图所示,在等腰△ABC中,AB=AC,CD是中线,延长AB到E,使得BE=AB,连结CE,求证:CD=$\frac{1}{2}$CE.