题目内容
5. 如图,在?ABCD中,∠BAD的平分线交DC于点E,若DE:EC=3:1,AB的长为8,AB边上的高线长为5,求BC与AD之间的距离.
如图,在?ABCD中,∠BAD的平分线交DC于点E,若DE:EC=3:1,AB的长为8,AB边上的高线长为5,求BC与AD之间的距离.
分析 由?ABCD的对边相等推知CD=AB=8,则易求DE=6;然后由?ABCD的对边相互平行证得DC∥AB,所以根据平行线的性质和角平分线的性质证得△ADE是等腰三角形,即AD=DE=6,再由平行四边形的面积即可求出结果.
解答 解:设BC与AD之间的距离为h,
∵四边形ABCD是平行四边形,
∴CD=AB=8.
又DE:EC=3:1,
∴DE=CD×$\frac{3}{4}$=6.∵DC∥AB,
∴∠DEA=∠BAE,
∵AE是∠A的平分线,
∴∠DAE=∠BAE,
∴∠DAE=∠DEA.
∴AE=ED=6.
∵平行四边形ABCD的面积=5×AB=6h,
∴h=$\frac{5×8}{6}$=$\frac{20}{3}$,
即BC与AD之间的距离为$\frac{20}{3}$.
点评 本题考查了平行四边形的性质.平行四边形的对边相等且平行.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
15.下列四个数中,比-1小的数是( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{3}$ |
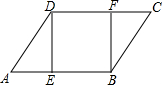 如图,已知在?ABCD中,DE⊥AB于E,BF⊥CD于F,AD=4.∠A=60°,求DE,FB的长.
如图,已知在?ABCD中,DE⊥AB于E,BF⊥CD于F,AD=4.∠A=60°,求DE,FB的长.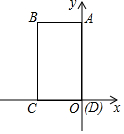 如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为(-6,4),(-6,2$\sqrt{7}$),(-6,8-2$\sqrt{7}$).
 如图.在?ABCD中,BE⊥DC于E,BF⊥DA于F,若∠A=30°,BE=6.BF=9.求?ABCD的面积和周长.
如图.在?ABCD中,BE⊥DC于E,BF⊥DA于F,若∠A=30°,BE=6.BF=9.求?ABCD的面积和周长. 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论的个数是( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论的个数是( )