题目内容
13.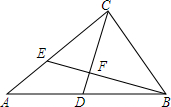 如图,在Rt△ABC中,∠ACB=90°,CD是中线.BE⊥CD交CA于点E,交CD于点F.
如图,在Rt△ABC中,∠ACB=90°,CD是中线.BE⊥CD交CA于点E,交CD于点F.(1)求证:$\frac{EF}{BF}$=$\frac{CE}{CA}$;
(2)如果CE=4cm,AE=2cm,求DF的长.
分析 (1)过A作AG∥BE交CD的延长线于G,于是得到∠GAD=∠FBD,推出△ADG≌△BFD,求得AG=BF,由△CEF∽△CAG,即可得到结论;
(2)由$\frac{EF}{BF}$=$\frac{CE}{CA}$=$\frac{4}{6}$=$\frac{2}{3}$,设EF=2k,AC=3k,通过△ECF∽△BCF,得到$\frac{EF}{CF}=\frac{CF}{BF}$,根据勾股定理得到CE2=EF2+CF2,求出CF=$\frac{4\sqrt{15}}{5}$,AG=BF=$\frac{6\sqrt{10}}{5}$,然后根据勾股定理得到CG=$\sqrt{A{C}^{2}-A{G}^{2}}$=$\frac{6\sqrt{15}}{5}$,即可得到结论.
解答 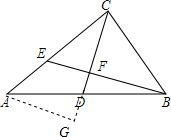 解:(1)过A作AG∥BE交CD的延长线于G,
解:(1)过A作AG∥BE交CD的延长线于G,
∴∠GAD=∠FBD,
在△ACD与△BDF中,
$\left\{\begin{array}{l}{∠GAD=∠FBD}\\{AD=BD}\\{∠ADG=∠BDF}\end{array}\right.$,
∴△ADG≌△BFD,
∴AG=BF,
∵AG∥BE,
∴△CEF∽△CAG,
∴$\frac{EF}{AG}=\frac{CE}{CA}$,
∴$\frac{EF}{BF}$=$\frac{CE}{CA}$;
(2)∵$\frac{EF}{BF}$=$\frac{CE}{CA}$=$\frac{4}{6}$=$\frac{2}{3}$,
设EF=2k,AC=3k,
∵∠ACB=90°,BE⊥CD交CA于点E,
∴∠ECF+∠BCF=∠BCF+∠CBF=90°,
∴∠ECF=∠CBF,
∴△ECF∽△BCF,
∴$\frac{EF}{CF}=\frac{CF}{BF}$,
∴CF=$\sqrt{6}$k,
∵CE2=EF2+CF2,
即16=4k2+6k2,
∴k=$\frac{2\sqrt{10}}{5}$,
∴CF=$\frac{4\sqrt{15}}{5}$,AG=BF=$\frac{6\sqrt{10}}{5}$,
∴CG=$\sqrt{A{C}^{2}-A{G}^{2}}$=$\frac{6\sqrt{15}}{5}$,
∴DF=$\frac{1}{2}$GF=$\frac{1}{2}$(CG-CF)=$\frac{\sqrt{15}}{5}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行线的性质,熟练掌握各定理是解题的关键.

| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | ±$\frac{2}{3}$ |
 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )| A. | b<a | B. | a+b<0 | C. | ab<0 | D. | b-a>0 |
①开口向下;②顶点是原点;③过点(6,-6).
| A. | y=-$\frac{1}{6}{x}^{2}$ | B. | y=$\frac{1}{6}{x}^{2}$ | C. | y=-6x2 | D. | y=6x2 |
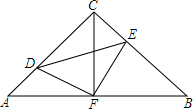 如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.
如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16. 如图,已知AB∥CD,直线EF交AB于点E,交CD于F,ME平分∠AEF、MF平分∠CFE,证明:ME⊥MF.
如图,已知AB∥CD,直线EF交AB于点E,交CD于F,ME平分∠AEF、MF平分∠CFE,证明:ME⊥MF.