题目内容
17.已知某二次函数满足下列条件,求其表达式.(1)图象经过点A(1,3),B(-2,12),C(-1,5)三点;
(2)图象经过点A(1,0),B(0,-3),且对称轴是直线x=2;
(3)图象与x轴交点的横坐标分别是-2和3,且函数有最小值-3.
分析 (1)设一般式为y=ax2+bx+c,然后把三个点的坐标代入得到a、b、c的方程组,再解方程组即可;
(2)利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为(3,0),则可设交点式y=a(x-1)(x-3),然后把(0,-3)代入求出a的值即可;
(3)利用抛物线对称性得到抛物线的对称轴为直线x=$\frac{1}{2}$,抛物线的顶点坐标为($\frac{1}{2}$,-3),设一般式y=a(x+2)(x-3),然后把顶点坐标代入求出a即可.
解答 解:(1)设抛物线解析式为y=ax2+bx+c,
根据题意得$\left\{\begin{array}{l}{a+b+c=3}\\{4a-2b+c=12}\\{a-b+c=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=-1}\\{c=2}\end{array}\right.$,
所以抛物线解析式为y=2x2-x+2;
(2)∵抛物线的对称轴是直线x=2,
∴抛物线与x轴的另一个交点坐标为(3,0),
设抛物线解析式为y=a(x-1)(x-3),
把(0,-3)代入得a•(-1)•(-3)=-3,解得a=-1,
所以抛物线解析式为y=-(x-1)(x-3),即y=-x2+4x-3;
(3)根据题意,抛物线与x轴的交点坐标为(-2,0),(3,0),
抛物线的对称轴为直线x=$\frac{1}{2}$,
所以抛物线的顶点坐标为($\frac{1}{2}$,-3),
设抛物线解析式为y=a(x+2)(x-3),
把($\frac{1}{2}$,-3)代入得a•$\frac{5}{2}$•(-$\frac{5}{2}$)=-3,解得a=$\frac{12}{25}$,
所以抛物线解析式为y=$\frac{12}{25}$(x-$\frac{1}{2}$)2-3.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

 如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.
如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.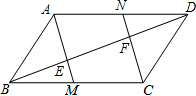 如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.
如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.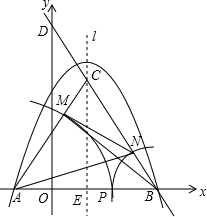 如图所示,抛物线y=-x2+2x+8与x轴交于A、B两点,直线BD的解析式为y=-2$\sqrt{3}x$+8$\sqrt{3}$,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.
如图所示,抛物线y=-x2+2x+8与x轴交于A、B两点,直线BD的解析式为y=-2$\sqrt{3}x$+8$\sqrt{3}$,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.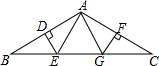 如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.
如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.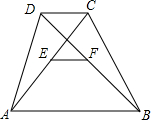 已知:如图,在四边形ABCD中,AB∥CD,AB>CD.E、F分别是AC、BD的中点.
已知:如图,在四边形ABCD中,AB∥CD,AB>CD.E、F分别是AC、BD的中点.