题目内容
12.观察下列一组分式:$\frac{y}{x}$,-$\frac{3y}{{x}^{2}}$,$\frac{7y}{{x}^{3}}$,-$\frac{13y}{{x}^{4}}$,$\frac{21y}{{x}^{5}}$…则第8个分式为-$\frac{57y}{{x}^{8}}$,第n个分式为$\frac{(n-1)n(-1)^{n+1}y}{{x}^{n}}$(n为正整数).分析 根据观察,可发现规律:第n项是$\frac{(n-1)n(-1)^{n+1}y}{{x}^{n}}$,可得答案.
解答 解:第8个分式为-$\frac{57y}{{x}^{8}}$,第n个分式为$\frac{(n-1)n(-1)^{n+1}y}{{x}^{n}}$,
故答案为:-$\frac{57y}{{x}^{8}}$,$\frac{(n-1)n(-1)^{n+1}y}{{x}^{n}}$.
点评 本题考查了分式的定义,现规律:第n项是$\frac{(n-1)n(-1)^{n+1}y}{{x}^{n}}$是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
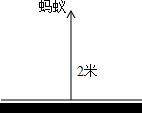 如图,蚂蚁在距巢穴2米远找到一只苍蝇,决定将其搬回家,可蚂蚁每一分钟内前进1米,却被风刮退2米,请问这只蚂蚁能否回到巢穴?如不能,请说明理由;如能,算一算何时能回巢穴.
如图,蚂蚁在距巢穴2米远找到一只苍蝇,决定将其搬回家,可蚂蚁每一分钟内前进1米,却被风刮退2米,请问这只蚂蚁能否回到巢穴?如不能,请说明理由;如能,算一算何时能回巢穴.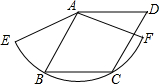 如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.
如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积. 已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?
已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?