题目内容
6.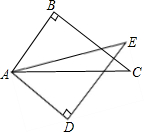 如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)
如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)
分析 条件是∠C=∠E,根据全等三角形的判定定理AAS推出即可.
解答 解:∠C=∠E,
理由是:在△ABC和△ADE中
∵$\left\{\begin{array}{l}{∠C=∠E}\\{∠B=∠C}\\{AB=AD}\end{array}\right.$
∴△ABC≌△ADE,
故答案为:∠C=∠E.
点评 本题考查了全等三角形的判定定理的应用,能运用定理得出答案是解此题的关键,此题是一道开放型的题目,答案不唯一.

练习册系列答案
相关题目
16. 如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
 如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )| A. | 当BC等于0.5时,l与⊙O相离 | B. | 当BC等于2时,l与⊙O相切 | ||
| C. | 当BC等于1时,l与⊙O相交 | D. | 当BC不为1时,l与⊙O不相切 |
18.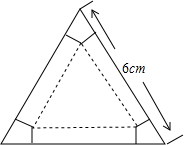 如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
 如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )| A. | $\sqrt{3}$cm2 | B. | $\frac{3}{2}$$\sqrt{3}$cm2 | C. | $\frac{9}{2}$$\sqrt{3}$cm2 | D. | $\frac{27}{2}$$\sqrt{3}$cm2 |
15. 如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
 如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )| A. | 转化思想 | |
| B. | 三角形的两边之和大于第三边 | |
| C. | 两点之间,线段最短 | |
| D. | 三角形的一个外角大于与它不相邻的任意一个内角 |
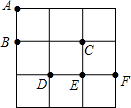 在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上. 如图,已知△ABC.
如图,已知△ABC.
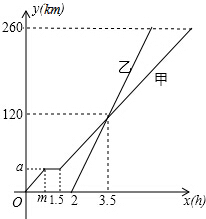 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )