题目内容
16. 如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )| A. | 当BC等于0.5时,l与⊙O相离 | B. | 当BC等于2时,l与⊙O相切 | ||
| C. | 当BC等于1时,l与⊙O相交 | D. | 当BC不为1时,l与⊙O不相切 |
分析 根据圆心到直线的距离大于半径,直线与圆相离,圆心到直线的距离小于半径,直线与圆相交;圆心到直线的距离等于半径,直线与圆相切,可得答案.
解答 解:A、∵BC=0.5,∴OC=OB+CB=1.5;∵∠AOB=60°,∴∠ACO=30°,AO=$\frac{1}{2}$OC=0.75<1,∴l与⊙O相交,故A错误;
B、∵BC=2,∴OC=OB+CB=3;∵∠AOB=60°,∴∠ACO=30°,AO=$\frac{1}{2}$OC=1.5>1,∴l与⊙O相离,故B错误;
C、∵BC=1,∴OC=OB+CB=2;∵∠AOB=60°,∴∠ACO=30°,AO=$\frac{1}{2}$OC=1,∴l与⊙O相切,故C错误;
D、∵BC≠1,∴OC=OB+CB≠2;∵∠AOB=60°,∴∠ACO=30°,AO=$\frac{1}{2}$OC≠1,∴l与⊙O不相切,故D正确;
故选:D.
点评 本题考查了直线与圆的位置关系,利用了直线与圆的位置关系:圆心到直线的距离大于半径,直线与圆相离;圆心到直线的距离小于半径,直线与圆相交;圆心到直线的距离等于半径,直线与圆相切.

练习册系列答案
相关题目
6.若(a-2)2+(b+3)2=0,则(a+b)2015的值是( )
| A. | 0 | B. | 1 | C. | -l | D. | 2012 |
7.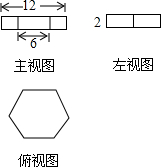 如图所示是某几何体的三视图,则该几何体的体积是( )
如图所示是某几何体的三视图,则该几何体的体积是( )
 如图所示是某几何体的三视图,则该几何体的体积是( )
如图所示是某几何体的三视图,则该几何体的体积是( )| A. | 18$\sqrt{3}$ | B. | 54$\sqrt{3}$ | C. | 108$\sqrt{3}$ | D. | 216$\sqrt{3}$ |
4.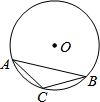 如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
 如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )| A. | $\sqrt{3}$cm | B. | $\frac{\sqrt{3}}{2}$cm | C. | $\frac{\sqrt{3}}{3}$cm | D. | 2$\sqrt{3}$cm |
11.在△ABC中,∠C=90°,sinA=$\frac{3}{5}$,D是AB的中点,则tan∠BCD+tan∠ACD=( )
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
1.下列运算中,正确的是( )
| A. | 3a+2a2=5a3 | B. | a•a4=a4 | C. | a6÷a3=a2 | D. | (-3x3)2=9x6 |
8.若x=-$\frac{1}{3}$,则|x|的值是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
 在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A(4,0)和B(0,2)
在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A(4,0)和B(0,2)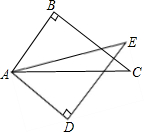 如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)
如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)