题目内容
16.某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
分析 (1)直接利用扇形统计图中百分数,进而求出B班参赛作品数量;
(2)利用C班提供的参赛作品的获奖率为50%,结合C班参赛数量得出获奖数量;
(3)分别求出各班的获奖百分率,进而求出答案;
(4)利用树状统计图得出所有符合题意的答案进而求出其概率.
解答 解:(1)由题意可得:100×(1-35%-20%-20%)=25(件),
答:B班参赛作品有25件;
(2)∵C班提供的参赛作品的获奖率为50%,
∴C班的参赛作品的获奖数量为:100×20%×50%=10(件),
如图所示: ;
;
(3)A班的获奖率为:$\frac{14}{100×35%}$×100%=40%,
B班的获奖率为:$\frac{11}{25}$×100%=44%,
C班的获奖率为:50%;
D班的获奖率为:$\frac{8}{100×20%}$×100%=40%,
故C班的获奖率高;
(4)如图所示: ,
,
故一共有12种情况,符合题意的有2种情况,
则从中一次随机抽出两张卡片,求抽到A、B两班的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题主要考查了树状图法求概率以及扇形统计图与条形统计图的应用,根据题意利用树状图得出所有情况是解题关键.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | 对角线相等且相互垂直的四边形是菱形 | |
| B. | 四条边相等的四边形是正方形 | |
| C. | 对角线相互垂直的四边形是平行四边形 | |
| D. | 对角线相等且相互平分的四边形是矩形 |
11.口袋里有红、蓝、绿的三种颜色小球,6个红球,5个绿球,若任意摸出一个绿球的概率是0.25,则任意摸出篮球的概率是多少?( )
| A. | 0.25 | B. | 0.4 | C. | 0.45 | D. | 0.5 |
8. 如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )
如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )
 如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )
如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )| A. | 1200m | B. | 1200$\sqrt{2}$m | C. | 1200$\sqrt{3}$m | D. | 2400m |
6.对于两个不相等的实数a、b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | 1-$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1+$\sqrt{2}$或-1 |
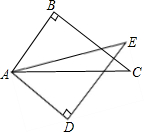 如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)
如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可) 已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于$\frac{9\sqrt{5}}{2}$.
已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于$\frac{9\sqrt{5}}{2}$.