题目内容
15. 如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )| A. | 转化思想 | |
| B. | 三角形的两边之和大于第三边 | |
| C. | 两点之间,线段最短 | |
| D. | 三角形的一个外角大于与它不相邻的任意一个内角 |
分析 利用两点之间线段最短分析并验证即可即可.
解答 解:∵点B和点B′关于直线l对称,且点C在l上,
∴CB=CB′,
又∵AB′交l与C,且两条直线相交只有一个交点,
∴CB′+CA最短,
即CA+CB的值最小,
将轴对称最短路径问题利用线段的性质定理两点之间,线段最短,体现了转化思想,验证时利用三角形的两边之和大于第三边.
故选D.
点评 此题主要考查了轴对称最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
7.下列说法正确的是( )
| A. | 对角线相等且相互垂直的四边形是菱形 | |
| B. | 四条边相等的四边形是正方形 | |
| C. | 对角线相互垂直的四边形是平行四边形 | |
| D. | 对角线相等且相互平分的四边形是矩形 |
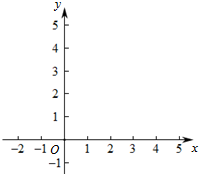 在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A(4,0)和B(0,2)
在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A(4,0)和B(0,2)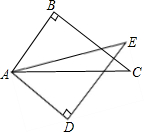 如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)
如图,在△ABC和△ADE中,∠B=∠D=90°,AB=AD,要使△ABC≌△ADE,应添加条件∠C=∠E.(添加一个条件即可)
 如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )
如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①$\frac{AG}{AB}$=$\frac{AF}{FC}$;②若点D是AB的中点,则AF=$\frac{\sqrt{2}}{3}$AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若$\frac{DB}{AD}$=$\frac{1}{2}$,则S△ABC=9S△BDF,其中正确的结论序号是( )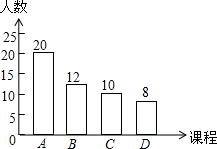 某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有800人.
某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有800人. 已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于$\frac{9\sqrt{5}}{2}$.
已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于$\frac{9\sqrt{5}}{2}$.