题目内容
9.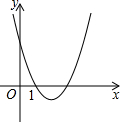 如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).
如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).
分析 把点(1,0)代入二次函数的解析式中,得到m的一元一次方程,求出m的值即可,再令y=0,求出x的值,即可求出抛物线与x轴的交点坐标.
解答 解:∵二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),
∴1-m+3=0,
∴m=4,
令x2-4x+3=0,
解得x1=3,x2=1,
即抛物线与x轴的交点坐标为(1,0)和(3,0);
与x轴另一个交点的坐标为(3,0);
故答案为4;(3,0).
点评 本题主要考查了抛物线与x轴的交点问题,解题的关键是掌握求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
18.点P(-2,5)关于y轴对称的点的坐标为( )
| A. | (2,-5) | B. | (5,-2) | C. | (-2,-5) | D. | (2,5) |
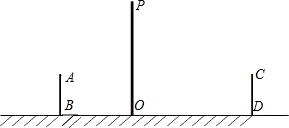 如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
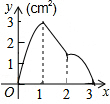
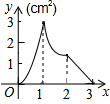
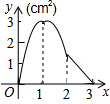
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.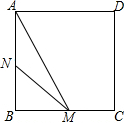 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )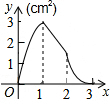
 国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题: