题目内容
17.计算:($\sqrt{3}+\sqrt{5}-\sqrt{7}$)($\sqrt{3}$-$\sqrt{5}$+$\sqrt{7}$)分析 先变形得到原式=[($\sqrt{3}$+($\sqrt{5}$-$\sqrt{7}$)][$\sqrt{3}$-($\sqrt{5}$-$\sqrt{7}$)],然后利用平方差公式和完全平方公式计算.
解答 解:原式=[($\sqrt{3}$+($\sqrt{5}$-$\sqrt{7}$)][$\sqrt{3}$-($\sqrt{5}$-$\sqrt{7}$)]
=($\sqrt{3}$)2-($\sqrt{5}$-$\sqrt{7}$)2
=3-(5-2$\sqrt{35}$+7)
=3-12+2$\sqrt{35}$
=-9+2$\sqrt{35}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
7. 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$的结果为( )
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$的结果为( )
 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$的结果为( )
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$的结果为( )| A. | -b | B. | 2a-b | C. | b-2a | D. | b |
6.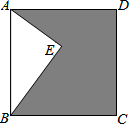 如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )
如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )
 如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )
如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )| A. | 76 | B. | 24 | C. | 48 | D. | 88 |
7. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | C. | π-$\frac{\sqrt{3}}{2}$ | D. | π-$\sqrt{3}$ |
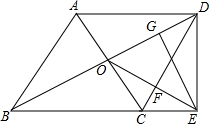 如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.
如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE. 如图所示,在Rt△ABC中,∠C=90°,D是BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,求AC的长.
如图所示,在Rt△ABC中,∠C=90°,D是BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,求AC的长.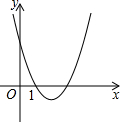 如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).
如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).