题目内容
4.一组数1,2,3,…,2012,是否可以在每个数之前添加“+”或“-”使所有数的和为2012,如果可以,请说明如何添加;如果不可以,试说明理由.分析 由2012是4的倍数,可将这组数4个一组分配,结合-1-2+3+4=4,即可得出每组数中前两为“-”,后两为“+”,即可得出结论.
解答 解:∵2012=503×4,
∴将1,2,3,…,2012,按4个一组分配.
∵-1-2+3+4=4,
∴-(4n+1)-(4n+2)+(4n+3)+(4n+4)=4,
∴每组数中前两为“-”,后两为“+”.
∴-1-2+3+4-5-…+2011+2012=4×503=2012.
点评 本题考查了规律型中得数字的变化类,解题的关键是根据-1-2+3+4=4找出“+”“-”号的分配方法.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
19. 如图所示是4×4的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中阴影部分是一个中心对称图形,这样的涂法有( )
如图所示是4×4的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中阴影部分是一个中心对称图形,这样的涂法有( )
 如图所示是4×4的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中阴影部分是一个中心对称图形,这样的涂法有( )
如图所示是4×4的正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中阴影部分是一个中心对称图形,这样的涂法有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
16.下列运算正确的是( )
| A. | a7÷a4=a3 | B. | 5a2-3a=2a | C. | 3a4•a2=3a8 | D. | (a3b2)2=a5b4 |
13.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2+a2=a4 | C. | 3a2×2a2=6a4 | D. | 5a-a=4 |
14.下列各式计算中,能用平方差公式计算的是( )
| A. | (4x-5y)(-5y-4x) | B. | (-4x+5y)(-5y+4x) | C. | (-4x-5y)(5y+4x) | D. | (4x-5y)(5y-4x) |
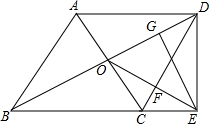 如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.
如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE. 如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).
如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).