题目内容
19. 国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:(1)此日历中能画出12个十字框?
(2)若a+b+c+d=84,求k的值;
(3)是否存在k的值,使得a+b+c+d=108,请说明理由.
分析 (1)直接利用已知图表分析得出符合题意的位置;
(2)利用日历中数据之间的关系进而得出k的值;
(3)利用日历中数据之间的关系进而分析得出答案.
解答 解:(1)由题意可得:十字框顶端分别在:1,2,5,6,7,8,9,12,13,14,15,16一共有12个位置,
故答案为:12;
(2)由题意可得:设最上面为a,最左边为b,最右边为c,最下面为d,
则b=a+6,c=a+8,d=a+14,k=a+7,
故a+a+6+a+8+a+14=84,
解得:a=14,
则k=21;
(3)不存在k的值,使得a+b+c+d=108,
理由:当a+b+c+d=108,
则a+a+6+a+8+a+14=108,
解得:a=20,故d=34>31(不合题意),
故不存在k的值,使得a+b+c+d=108.
点评 此题主要考查了一元一次方程的应用,正确得出日历中数据之间的关系是解题关键.

练习册系列答案
相关题目
10.计算2x2y(x-3xy2)=( )
| A. | 2x3y-3x3y3 | B. | 2xy2-6x3y3 | C. | 2x3y-6x3y3 | D. | 2x2y+6x3y3 |
7. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ | C. | π-$\frac{\sqrt{3}}{2}$ | D. | π-$\sqrt{3}$ |
14.下列各式计算中,能用平方差公式计算的是( )
| A. | (4x-5y)(-5y-4x) | B. | (-4x+5y)(-5y+4x) | C. | (-4x-5y)(5y+4x) | D. | (4x-5y)(5y-4x) |
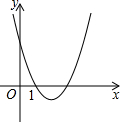 如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0).
如图,二次函数y=x2-mx+3的图象与x轴的一个交点为(1,0),则m的值为4,与x轴另一个交点的坐标为(3,0). 如图,在平面直角坐标系中,A($\sqrt{3}$,0),B($\sqrt{3}$,1),将△OAB绕点O逆时针旋转至△OA′B′,使点B的对应点B′,落在y轴的正半轴上.
如图,在平面直角坐标系中,A($\sqrt{3}$,0),B($\sqrt{3}$,1),将△OAB绕点O逆时针旋转至△OA′B′,使点B的对应点B′,落在y轴的正半轴上.