��Ŀ����
���õķֽ���ʽ�ķ�������ȡ����ʽ������ʽ����ʮ����˷���������Щ����ʽ���ֻ���������������ֽ⣬��x2-4y2-2x+4y������ϸ�Ĺ۲����ʽ�Ӿͻᷢ�֣�ǰ�������ƽ���ʽ�����������ȡ����ʽ��ǰ�������ֱַ�ֽ���ʽ����������ʽ��Ȼ����ȡ����ʽ�Ϳ����������ʽ�ӵķֽ���ʽ�ˣ�����Ϊ��x2-4y2-2x+4y=��x+2y����x-2y��-2��x-2y��=��x-2y����x+2y-2�������ַֽ���ʽ�ķ����з���ֽⷨ���������ַ�������������⣺
��1���ֽ���ʽ��x2-9y2-2x+6y��
��2���ֽ���ʽ��x2-8xy+16y2-1��
��3����ABC����a��b��c ����a2-ab-ac+bc=0���жϡ�ABC����״��
��1���ֽ���ʽ��x2-9y2-2x+6y��
��2���ֽ���ʽ��x2-8xy+16y2-1��
��3����ABC����a��b��c ����a2-ab-ac+bc=0���жϡ�ABC����״��
���㣺��ʽ�ֽ��Ӧ��
ר�⣺
��������1�����Ƚ�ǰ������ϣ�����ƽ���ʽ�ֽ���ʽ�����������ṫ��ʽ�ֽ���ʽ�ó����ɣ�
��2�����Ƚ�ǰ������ϣ�������ȫƽ����ʽ�ֽ���ʽ����������ƽ���ʽ�ֽ���ʽ�ó����ɣ�
��3�����Ƚ�ǰ�����Լ���������ϣ�������ȡ����ʽ���ֽ���ʽ�����ɵó�a��b��c�Ĺ�ϵ���ж���������״���ɣ�
��2�����Ƚ�ǰ������ϣ�������ȫƽ����ʽ�ֽ���ʽ����������ƽ���ʽ�ֽ���ʽ�ó����ɣ�
��3�����Ƚ�ǰ�����Լ���������ϣ�������ȡ����ʽ���ֽ���ʽ�����ɵó�a��b��c�Ĺ�ϵ���ж���������״���ɣ�
����⣺��1��x2-9y2-2x+6y
=��x-3y����x+3y��-2��x-3y��
=��x-3y����x+3y-2����
��2��x2-8xy+16y2-1
=��x-4y��2-12
=��x-4y+1����x-4y-1����
��3����a2-ab-ac+bc=0
��a��a-b��-c��a-b��=0��
�ࣨa-b����a-c��=0��
��a=b��a=c��
���ABC����״�ǵ��������Σ�
=��x-3y����x+3y��-2��x-3y��
=��x-3y����x+3y-2����
��2��x2-8xy+16y2-1
=��x-4y��2-12
=��x-4y+1����x-4y-1����
��3����a2-ab-ac+bc=0
��a��a-b��-c��a-b��=0��
�ࣨa-b����a-c��=0��
��a=b��a=c��
���ABC����״�ǵ��������Σ�
������������Ҫ�����˷���ֽⷨ�ֽ���ʽ�Լ����������ε��ж�����ȷ����ֽ�ó��ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
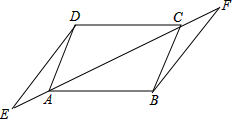 ��ͼ��AD��BC��AE=CF��AD=BC����E��F��ֱ��AC�ϣ��Բ����߶�DE��BF�кι�ϵ����˵����IJ��룮
��ͼ��AD��BC��AE=CF��AD=BC����E��F��ֱ��AC�ϣ��Բ����߶�DE��BF�кι�ϵ����˵����IJ��룮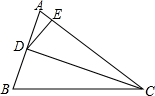 ��ͼ��CD�ǡ�ABC�С�ACB��ƽ���ߣ�E��AC�ϵ�һ�㣬��CD2=BC•CE��AD=6��AE=4��
��ͼ��CD�ǡ�ABC�С�ACB��ƽ���ߣ�E��AC�ϵ�һ�㣬��CD2=BC•CE��AD=6��AE=4�� �ı���ABCD�У�AB=BC��BE�AAD����ΪE����BCD-��ABE=90�㣮����C��CF��AD���Խ���BD��F����֤��CF=CD��
�ı���ABCD�У�AB=BC��BE�AAD����ΪE����BCD-��ABE=90�㣮����C��CF��AD���Խ���BD��F����֤��CF=CD��