题目内容
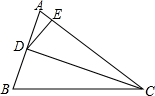 如图,CD是△ABC中∠ACB的平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.
如图,CD是△ABC中∠ACB的平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.(1)求证:△BCD∽△DCE.
(2)求AC的长.
考点:相似三角形的判定与性质
专题:
分析:(1)CD2=BC•CE,即
=
,然后根据两边的比相等,且夹角相等的两个三角形相似,即可证得;
(2)首先证明△ACD∽△ADE,根据相似三角形的对应边的比相等即可证得.
| CD |
| BC |
| CE |
| CD |
(2)首先证明△ACD∽△ADE,根据相似三角形的对应边的比相等即可证得.
解答:(1)证明:∵CD2=BC•CE,
∴
=
,
又∵∠BCD=∠ACD,
∴△BCD∽△DCE;
(2)解:∵△BCD∽△DCE,
∴∠BDC=∠DEC,
又∵∠BDC=∠ACD+∠A,∠DEC=∠ADE+∠A,
∴∠ADE=∠ACD,
又∵∠A=∠A,
∴△ACD∽△ADE,
∴
=
,即
=
,
解得:AC=
.
∴
| CD |
| BC |
| CE |
| CD |
又∵∠BCD=∠ACD,
∴△BCD∽△DCE;
(2)解:∵△BCD∽△DCE,
∴∠BDC=∠DEC,
又∵∠BDC=∠ACD+∠A,∠DEC=∠ADE+∠A,
∴∠ADE=∠ACD,
又∵∠A=∠A,
∴△ACD∽△ADE,
∴
| AD |
| AE |
| AC |
| AD |
| 6 |
| 4 |
| AC |
| 6 |
解得:AC=
| 9 |
| 2 |
点评:本题考查了相似三角形的判定与性质,证明∠ADE=∠ACD是关键.

练习册系列答案
相关题目
 如图,∠B=49°,AB∥CE,∠E=∠D,求:∠E,∠D.
如图,∠B=49°,AB∥CE,∠E=∠D,求:∠E,∠D.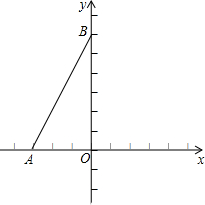 已知A(-3,0),B(0,6),通过原点O的直线把△OAB分为面积为1:3的两部分,求这条直线的函数解析式.
已知A(-3,0),B(0,6),通过原点O的直线把△OAB分为面积为1:3的两部分,求这条直线的函数解析式.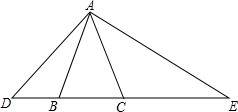 已知,如图,△ABC为等腰三角形,AB=AC,在不添加辅助线的条件下:
已知,如图,△ABC为等腰三角形,AB=AC,在不添加辅助线的条件下: