题目内容
12.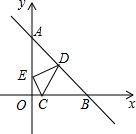 如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.
如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.
分析 点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,可以证明这个最小值就是线段C′C″.
解答 解:如图,点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″,
∵直线AB的解析式为y=-x+7,
∴直线CC″的解析式为y=x-1,
由$\left\{\begin{array}{l}{y=-x+7}\\{y=x-1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
∴E(4,3),
∵E是CC″中点,
∴可得C″(7,6).
连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C″=$\sqrt{{8}^{2}+{6}^{2}}$=10.
故答案为10.
点评 本题考查轴对称-最短问题、两点之间距离公式等知识,解题的关键是利用对称性在找到点D、点E位置,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列命题是假命题的是( )
| A. | 经过两点有且只有一条直线 | |
| B. | 三角形的中位线平行且等于第三边的一半 | |
| C. | 平行四边形的对角线相等 | |
| D. | 圆的切线垂直于经过切点的半径 |
20. 如图,点A、B、C都在⊙O上,若∠ACB=29°,则∠AOB的度数为( )
如图,点A、B、C都在⊙O上,若∠ACB=29°,则∠AOB的度数为( )
 如图,点A、B、C都在⊙O上,若∠ACB=29°,则∠AOB的度数为( )
如图,点A、B、C都在⊙O上,若∠ACB=29°,则∠AOB的度数为( )| A. | 14.5° | B. | 29° | C. | 58° | D. | 61° |
7.如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A($\frac{5}{3}$,0),B(0,4),则点B2016的横坐标为( )


| A. | 5 | B. | 12 | C. | 10070 | D. | 10080 |
2. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )| A. | 25° | B. | 40° | C. | 50° | D. | 65° |
 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=2$\sqrt{2}$.
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=2$\sqrt{2}$.