题目内容
2. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )| A. | 25° | B. | 40° | C. | 50° | D. | 65° |
分析 首先连接OC,由∠A=25°,可求得∠BOC的度数,由CD是圆O的切线,可得OC⊥CD,继而求得答案.
解答 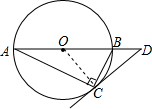 解:连接OC,
解:连接OC,
∵圆O是Rt△ABC的外接圆,∠ACB=90°,
∴AB是直径,
∵∠A=25°,
∴∠BOC=2∠A=50°,
∵CD是圆O的切线,
∴OC⊥CD,
∴∠D=90°-∠BOC=40°.
故选B.
点评 此题考查了切线的性质以及圆周角的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
13. 如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
 如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )| A. | 58° | B. | 42° | C. | 32° | D. | 28° |
7.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
| A. | 1或-5 | B. | -1或5 | C. | 1或-3 | D. | 1或3 |
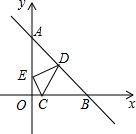 如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.
如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.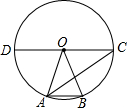 如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=35度.
如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=35度.
 设函数y=$\frac{k}{x}$(k≠0,x>0)的图象如图所示,若z=$\frac{1}{y}$,则z关于x的函数图象可能为( )
设函数y=$\frac{k}{x}$(k≠0,x>0)的图象如图所示,若z=$\frac{1}{y}$,则z关于x的函数图象可能为( )



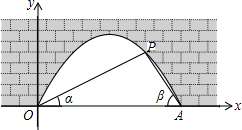 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tan$β=\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.
图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tan$β=\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.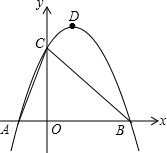 已知:如图,抛物线y=ax2+bx+3交x轴于A(-1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接AC,BC.
已知:如图,抛物线y=ax2+bx+3交x轴于A(-1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接AC,BC.