题目内容
17. 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=2$\sqrt{2}$.
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=2$\sqrt{2}$.
分析 连接BC可得RT△ACB,由勾股定理求得BC的长,进而由tanD=tanA=$\frac{BC}{AC}$可得答案.
解答 解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,AC=2,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
又∵∠D=∠A,
∴tanD=tanA=$\frac{BC}{AC}$=$\frac{4\sqrt{2}}{2}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了三角函数的定义、圆周角定理、解直角三角形,连接BC构造直角三角形是解题的关键.

练习册系列答案
相关题目
3.受“乡村旅游第一市”的品牌效应和2015年国际乡村旅游大会的宣传效应的影响,2016年湖州市在春节黄金周期间共接待游客约2800000人次,同比增长约56%,将2800000用科学记数法表示应是( )
| A. | 28×105 | B. | 2.8×106 | C. | 2.8×105 | D. | 0.28×105 |
8. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |
5.如图,AB是半圆O的直径,∠DBA=20°,则∠C的大小是( )

| A. | 70° | B. | 100° | C. | 110° | D. | 140° |
7.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
| A. | 1或-5 | B. | -1或5 | C. | 1或-3 | D. | 1或3 |
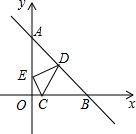 如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.
如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.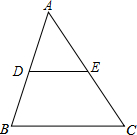 如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.
如图,△ABC的面积为12cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为9cm2.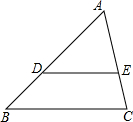 如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB=2.
如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB=2.