题目内容
3.在△ABC中,∠C=90°,D是AC上的点,∠A=∠DBC,将线段BD绕点B旋转,使点D落在线段AC的延长线上点D1处,已知BC:AC=1:2,则cos∠AD1B的值等于$\frac{\sqrt{5}}{5}$.分析 由∠A=∠DBC、∠C=90°可得到△ACB∽△BDC,由此得出DC:BC=BC:AC=1:2,通过旋转得到△BDD1为等腰三角形,利用角度转换就可以得出cos∠AD1B的值.
解答 解:如图所示: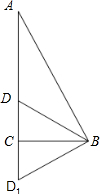
∵∠C=90°,∠A=∠DBC,
∴△ACB∽△BDC,
∴BC:AC=DC:AC,
∵BC:AC=1:2,
∴DC:AC=1:2,
设DC为a,则BC=2a
∴DB=$\sqrt{{a}^{2}+(2a)^{2}}$=$\sqrt{5}$a
∵BD绕点B旋转到BD1
∴BD=BD1,
∴∠AD1B=∠BDC
∴cos∠AD1B=cos∠BDC=a:$\sqrt{5}$a=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查了旋转的性质、相似三角形性质、勾股定理及三角函数,解题的关键是要利用旋转得出∠AD1B=∠BDC,实现了对所求角三角函数的转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列图形中,可以看作是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8. 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
 如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )
如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=50°,则∠BCE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |
15.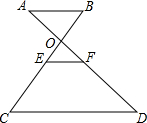 如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )
如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )
 如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )
如图,AB∥EF∥CD,BC、AD相交于点O,F是AD的中点,则下列结论中错误的是( )| A. | $\frac{AO}{AD}$=$\frac{BO}{BC}$ | B. | $\frac{OB}{CE}$=$\frac{OA}{DF}$ | C. | $\frac{EF}{CD}$=$\frac{OE}{BE}$ | D. | $\frac{2BE}{AD}$=$\frac{OE}{OF}$ |
13. 如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
 如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )| A. | 58° | B. | 42° | C. | 32° | D. | 28° |
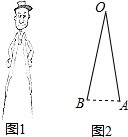 如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.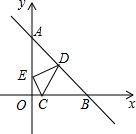 如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.
如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是10.