题目内容
17.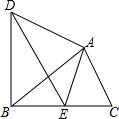 如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.
如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.(1)若∠C=65°,求∠DEB的度数;
(2)若∠BAC=90°,线段BC与BD有何关系?为什么?
分析 (1)根据旋转的性质可得∠C=∠AED=65°,AC=AE,根据等边对等角得出∠AEC=∠C=65°,然后根据平角的定义即可求出∠DEB的度数;
(2)根据旋转的性质可得∠BAD=∠CAE,AB=AD,AC=AE,再利用等腰三角形两底角相等表示出∠C、∠ABD,然后求出∠DBC=90°,根据垂直的定义即可得BC⊥BD.
解答  解:(1)∵△ABC绕点A顺时针旋转得△ADE,
解:(1)∵△ABC绕点A顺时针旋转得△ADE,
∴∠C=∠AED=65°,AC=AE,
∴∠AEC=∠C=65°,
∴∠DEB=180°-∠AEC-∠AED=180°-65°-65°=50°;
(2)线段BC⊥BD.理由如下:
∵△ABC绕点A顺时针旋转得△ADE,
∴∠BAD=∠CAE,AB=AD,AC=AE,
∴∠ABD=∠ADB=$\frac{1}{2}$(180°-∠BAD),∠C=∠AEC=$\frac{1}{2}$(180°-∠CAE),
∴∠ABD=∠C,
∵∠BAC=90°,
∴∠C+∠ABC=180°-90°=90°,
∴∠DBC=∠ABD+∠ABC=∠C+∠ABC=90°,
∴BC⊥BD.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰三角形两底角相等的性质,垂直的定义,熟练掌握旋转的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知x=$\frac{1}{1+\sqrt{2}}$,y=$\frac{1}{1-\sqrt{2}}$,则$\sqrt{3{x}^{2}-5xy+3{y}^{2}}$的值是$\sqrt{23}$.
2.下列事件中,属于必然事件的是( )
| A. | 明天会下雨 | |
| B. | 小强期末数学考试会得100分 | |
| C. | 深圳冬天会下雪 | |
| D. | 从一个只装有10个红球的袋子里任意摸出一个刚好是红球 |
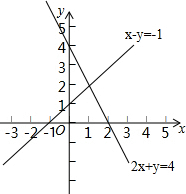 直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$. 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.