题目内容
17.风驰汽车销售公司12月份销售某型号汽车,进价为30万元/辆,售价为32万元/辆,当月销售量为x辆(x≤30,且x为正整数),销售公司有两种进货方案供选择:方案一:当x不超过5时,进价不变;当x超过5时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆(比如,当x=8时,该型号汽车的进价为29.7万元/辆);
方案二:进价始终不变,当月每销售1辆汽车,生产厂另外返还给销售公司1万元/辆.
(1)按方案一进货:
①当x=11时,该型号汽车的进价为29.4万元/辆;
②当x>5时,写出进价y(万元/辆)与x(辆)的函数关系式;
(2)当月该型号汽车的销售量为多少辆时,选用方案一和方案二销售公司获利相同?
(注:销售利润=销售价-进价+返利).
分析 (1)①当x=11时,该型号汽车的进价为:30-0.1×(11-5),再计算即可,
②当x>5时,进价y(万元/辆)与x(辆)的函数关系式:y=30-0.1×(x-5),再整理即可,
(2)设当月该型号汽车的销售量为x辆时,选用方案一和方案二销售公司获利相同,根据列出方程x[32-(30.5-0.1x)]=3x,最后求解即可.
解答 解:(1)①当x=11时,该型号汽车的进价为:
30-0.1×(11-5)=29.4万元/辆,
故答案为:29.4,
②当x>5时,进价y(万元/辆)与x(辆)的函数关系式:
y=30-0.1×(x-5)=30.5-0.1x,
(2)设当月该型号汽车的销售量为x辆时,选用方案一和方案二销售公司获利相同,根据题意得:
x[32-(30.5-0.1x)]=3x
解得:x1=0(舍去),x2=15.
答:该月售出15辆汽车时,选用方案一和方案二销售公司获利相同.
点评 此题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
8.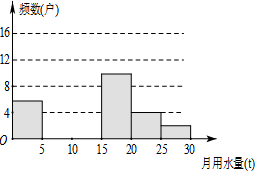 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
请解答以下问题:
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | n |
| 60≤x<70 | 2 | 0.04 |
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
6.化简-$\sqrt{-{x}^{3}}$的结果是( )
| A. | x$\sqrt{-x}$ | B. | -x$\sqrt{-x}$ | C. | x$\sqrt{x}$ | D. | -x$\sqrt{x}$ |
 如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上.
如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上.