题目内容
1．已知$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+by=2}\\{by+cz=3}\\{cx+az=7}\end{array}\right.$的解，则a+b+c的值是（ ）| A． | 3 | B． | 2 | C． | 1 | D． | 无法确定 |
分析 由题意，可将x，y及z的值代入方程组得到关于a，b，c的方程组，将方程组中三个方程左右两边相加，变形后即可求出a+b+c的值．
解答 解：由题意将$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$代入方程组得：
$\left\{\begin{array}{l}{a+2b=2①}\\{2b+3c=3②}\\{c+3a=7③}\end{array}\right.$，
①+②+③得：a+2b+2b+3c+c+3a=2+3+7，
即4a+4b+4c=4（a+b+c）=12，
则a+b+c=3．
故选A．
点评 此题考查了三元一次方程组的解，以及解三元一次方程组，方程组的解为能使方程组中每一个方程左右两边相等的未知数的值，本题的技巧性比较强，求a+b+c不要求出a，b及c的值，而是整体求出．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．若a＞b，则下列式子中错误的是（ ）
| A． | a-2＞b-2 | B． | -2a＞-2b | C． | 2a＞2b | D． | $\frac{a}{2}$＞$\frac{b}{2}$ |
如图，已知直线AE∥BC，AD平分∠BAE，交BC于点C，∠BCD=140°，则∠B的度数为100°．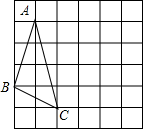
在下面的网格图中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B，C两点的坐标分被为（-1，-1），（1，-2），将△ABC绕着点C顺时针旋转90°，则点A的对应点的坐标为（5，-1）．
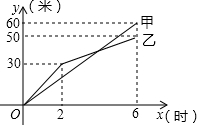某市创建文明城区的活动中，有两段长度相等的彩色道转铺设任务，分别交给甲、乙两个施工队同时进行施工，如图是反映所铺设彩色道转的长度y（米）与施工时间x（时）之间关系的部分图象，请解答下列问题：
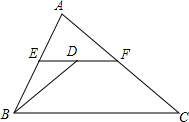如图，EF为△ABC的中位线，BD平分∠ABC，交EF于D，AB=8，BC=12，则DF的长为2．