题目内容
6.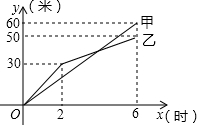 某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题:
某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题:(1)求乙队在0≤x≤2的时段内的施工速度;
(2)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)要施工多长时间甲、乙两队所铺设彩色道砖的长度刚好相等?
分析 (1)根据函数图象可以得到乙队在0≤x≤2的时段内的施工速度;
(2)根据乙队在2≤x≤6的时段内,函数图象为线段且经过点(2,30),(6,50),从而可以求出y与x之间的函数关系式;
(3)根据函数图象可以求得甲队对应的函数解析式,让甲乙两个函数解析式相等可以求得相应的x的值,本题得以解决.
解答 解:(1)由图象可得,
乙队在0≤x≤2的时段内的施工速度是:30÷2=15米/时;
(2)乙队在2≤x≤6的时段内,设y与x之间的函数关系式是y=kx+b,
则$\left\{\begin{array}{l}{2k+b=30}\\{6k+b=50}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=5}\\{b=20}\end{array}\right.$,
即乙队在2≤x≤6的时段内,y与x之间的函数关系式是y=5x+20;
(3)设甲队的函数解析式为y=ax,
则6a=60得a=10,
即甲队的函数解析式为y=10x,
10x=5x+20,
解得,x=4,
即要施工4小时时甲、乙两队所铺设彩色道砖的长度刚好相等.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出下面的表格:
根据表格提供的信息,下列说法错误的是( )
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
| A. | 该抛物线的对称轴是直线x=-2 | |
| B. | 该抛物线与y轴的交点坐标为(0,-2.5) | |
| C. | b2-4ac=0 | |
| D. | 若点A(0.5,y1)是该抛物线上一点.则y1<-2.5 |
14. 某星期天下午,小强和同学小颖相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小颖到了后两人一起乘公共汽车回学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,下列说法中错误的是( )
某星期天下午,小强和同学小颖相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小颖到了后两人一起乘公共汽车回学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,下列说法中错误的是( )
 某星期天下午,小强和同学小颖相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小颖到了后两人一起乘公共汽车回学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,下列说法中错误的是( )
某星期天下午,小强和同学小颖相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小颖到了后两人一起乘公共汽车回学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,下列说法中错误的是( )| A. | 小强乘公共汽车用了20分钟 | |
| B. | 小强在公共汽车站等小颖用了10分钟 | |
| C. | 公共汽车的平均速度是30公里/小时 | |
| D. | 小强从家到公共汽车站步行了2公里 |
18.不等式2x+3≤5x的解集在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
16.某篮球队5名主力队员的身高(单位:cm)分别是174,179,180,174,178,则这5名队员身高的中位数是( )
| A. | 174 | B. | 177 | C. | 178 | D. | 180 |
 如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的面积为$\frac{49\sqrt{3}}{2}$.
如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的面积为$\frac{49\sqrt{3}}{2}$. 如图,菱形ABCD,∠D=120°,E为菱形内一点,连结EC、EB.再将EB绕着点B逆时针旋转120°到FB,连结FA、EF,且EF交AB于点G.
如图,菱形ABCD,∠D=120°,E为菱形内一点,连结EC、EB.再将EB绕着点B逆时针旋转120°到FB,连结FA、EF,且EF交AB于点G.