题目内容
11.六一儿童节,某学习用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.其中,书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)分别写出两种优惠方法购买费用y1,y2(元)与所买水性笔支数x(支)的函数解析式(请化简函数解析式),并写出自变量x的取值范围;
(2)对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜.
分析 (1)根据“购买费用=购买书包钱数+购买水性笔钱数”即可得出两种优惠方法购买费用y1,y2(元)与所买水性笔支数x(支)的函数解析式;
(2)分别令y1=y2、y1>y2、y1<y2得出关于x的一元一次方程或一元一次不等式,解方程或不等式即可得出结论.
解答 解:(1)由题意可知:y1=(x-4)×5+20×4=5x+60(x≥4);
y2=(5x+20×4)×0.9=4.5x+72(x≥4).
(2)当y1=y2时,即5x+60=4.5x+72,
解得:x=24,
此时选择优惠方法①,②均可;
当y1>y2时,即5x+60>4.5x+72,
解得:x>24,
此时选择优惠方法②比较便宜;
当y1<y2时,即5x+60<4.5x+72,
解得:x<24,
此时选择优惠方法①比较便宜.
答:当购买水性笔数量x>24选择优惠方法②;当购买水性笔数量x=24时,选择优惠方法①,②均可;当购买水性笔数量4≤x<24选择优惠方法①.
点评 本题考查了一次函数的应用、解一元一次方程以及解一元一次不等式,解题的关键是:(1)根据数量关系列出函数解析式;(2)根据y1,y2间的关系列出方程或不等式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出函数关系式(方程或不等式)是关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
2. 如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
 如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )| A. | 58° | B. | 42° | C. | 32° | D. | 22° |
19.若a>b,则下列式子正确的是( )
| A. | -3a>-3b | B. | a-3>b-3 | C. | $\frac{3-a}{2}$>$\frac{3-b}{2}$ | D. | a+3b<4b |
16.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出下面的表格:
根据表格提供的信息,下列说法错误的是( )
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
| A. | 该抛物线的对称轴是直线x=-2 | |
| B. | 该抛物线与y轴的交点坐标为(0,-2.5) | |
| C. | b2-4ac=0 | |
| D. | 若点A(0.5,y1)是该抛物线上一点.则y1<-2.5 |
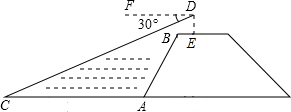 如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)
如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)