题目内容
10.已知:如图,Rt△ABC中,∠ACB=90°,AC=BC=8cm,O是AB中点,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CA运动,到点C、A时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则能表示S与t函数关系的图象大致是( )| A. | 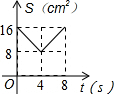 | B. | 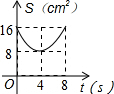 | C. | 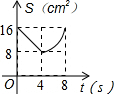 | D. | 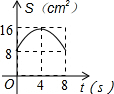 |
分析 根据等腰直角三角形的性质,中点的定义,推出三角形全等,然后由三角形的面积公式列出方程求出函数的解析式,由函数的解析式判断其函数的图形.
解答  解:如图,连接OC,由题意得:CF=BE=t,
解:如图,连接OC,由题意得:CF=BE=t,
∵∠ACB=90°,AC=BC=8cm,
∴AB=8$\sqrt{2}$,∠A=∠B=45°,
∵O是AB中点,
∴OA=OB=OC,∠OCF=45°,
在△OCF与△OBE中,$\left\{\begin{array}{l}{CF=BE}\\{∠ACO=∠B}\\{OC=OB}\end{array}\right.$,
∴△OCF≌△OBE,
∴S四边形CFOE=S△BOC=16,
∴S△FOE=S四边形CFOE-S△CEF=16=$\frac{1}{2}$t(8-t),
∴S=$\frac{1}{2}$t2-4t+16,
化为顶点式:S=$\frac{1}{2}$(t-4)2+8,
∴顶点坐标为(4,8),
故选B.
点评 本题考查了等腰直角三角形的性质,全等三角形的判定与性质,动点问题,二次函数的性质,证明三角形全等是解题的关键.

练习册系列答案
相关题目
13.下列各式中,计算结果为a6的是( )
| A. | a2+a4 | B. | (a2)4 | C. | a2•a3 | D. | a7÷a |
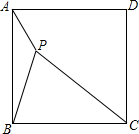 如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3, 如图,在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.
如图,在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.