题目内容
20.如图①,在平行四边形ABCD中,AD=9cm,动点P从A点出发,以1cm/s的速度沿着A→B→C→A的方向移动,直到点P到达点A后才停止.已知△PAD的面积y(单位:cm2)与点P移动的时间x(单位:s)之间的函数关系如图②所示,图②中a与b的和为55.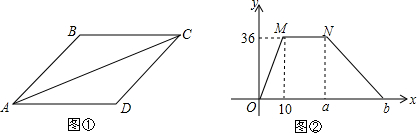
分析 由图②知点P在AB上运动的时间为10s,根据列出=速度×时间,求出AB=10cm,由AD=9cm可知点P在边BC上的运动时间为9s,a为点P由A→B→C的时间;分别过B点、C点作BE⊥AD、CF⊥AD,易证△BAE≌△CDF,由此得到AE=DF=6,AF=15,从而可求得CA=17s,则点P在CA边上从C点运动到A点的时间为17,所以b=19+17=36;再相加即可求解.
解答  解:由图②可知点P从A点运动到B点的时间为10s,
解:由图②可知点P从A点运动到B点的时间为10s,
又因为P点运动的速度为1cm/s,
所以AB=10×1=10(cm),
由AD=9可知点P在边BC上的运动时间为9s,
所以a=10+9=19;
分别过B点、C两点作BE⊥AD于E,CF⊥AD于F.
由图②知S△ABD=36,
则$\frac{1}{2}$×9×BE=36,
解得BE=8,
在直角△ABE中,由勾股定理,得AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=6.
易证△BAE≌△CDF,
则BE=CF=8,AE=DF=6,AF=AD+DF=9+6=15.
在直角△ACF中,由勾股定理,得CA=$\sqrt{A{F}^{2}+C{F}^{2}}$=17,
则点P在CA边上从C点运动到A点的时间为17s,
所以b=19+17=36,
a+b=19+36=55.
故答案为:55.
点评 本题考查了动点问题的函数图象,根据图②的三角形的面积的变化情况求出AB的长度是解题的关键,在梯形的问题中,作梯形的高是一种常用的辅助线的作法.

练习册系列答案
相关题目
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)( )
| A. | 36,8 | B. | 28,6 | C. | 28,8 | D. | 13,3 |
12.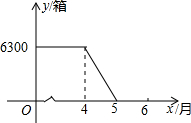 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
求:有几种购买设备的方案?若为了使日产量最大,应选择怎样的方案?
 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.(1)从图象可知,该厂5月份开始出现零库存:此时日产销量为500箱;
(2)4月份总共的销售量为21300箱;
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于4月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
| 型号 | A | B |
| 价格(万元/台) | 28 | 25 |
| 日产量(箱/台) | 50 | 40 |
9.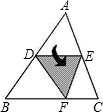 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )| A. | 55° | B. | 60° | C. | 70° | D. | 不能确定 |
 在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得AO=18m,BO=21m,延长AO,BO分别到D,C两点,使OC=6m,OD=7m,又测得CD=5m,则河塘宽AB=15m.
在综合实践课上,小明同学设计了如图测河塘宽AB的方案:在河塘外选一点O,连结AO,BO,测得AO=18m,BO=21m,延长AO,BO分别到D,C两点,使OC=6m,OD=7m,又测得CD=5m,则河塘宽AB=15m.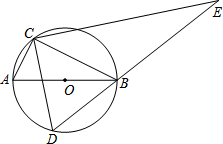 如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.
如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.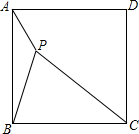 如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,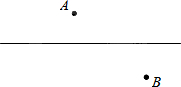 如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?