题目内容
17.已知△ABC与△A′B′C′的相似比为1:2,△ABC的周长为30cm,并且△A′B′C′的三边比为4:5:6,则△A′B′C′的最长边为( )| A. | 44cm | B. | 40cm | C. | 36cm | D. | 24cm |
分析 根据相似三角形的性质求出△A′B′C′的周长,再根据三边占的比值求出即可.
解答 解:∵△ABC与△A′B′C′的相似比为1:2,△ABC的周长为30cm,
∴△A′B′C′的周长为60cm,
∵△A′B′C′的三边比为4:5:6,
∴△A′B′C′的最长边为:$\frac{6}{4+5+6}$×60cm=24cm,
故选D.
点评 本题考查了相似三角形的性质的应用,能求出△A′B′C′的周长是解此题的关键,注意:三角形的周长比等于相似比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.某商店出售某商品时,在进价的基础上加一定的利润,其数量x与售价y的关系如下表所示.请根据表中所提供的信息,列出y与x之间的函数关系式,并求出当数量是2.5千克时的售价.
| 数量x(千克) | 1 | 2 | 3 | 4 | … |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
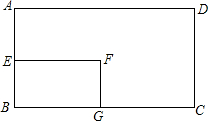 如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )
如图,矩形ABCD的面积是72,AE=$\frac{1}{2}$DC,EF=$\frac{1}{2}$AD,那么矩形EBGF的面积是( )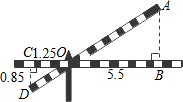 如图,铁道口的栏杆的短臂长1.25米,长臂长5.5米,当短臂端点下降0.85米时,长臂端点升高多少米?
如图,铁道口的栏杆的短臂长1.25米,长臂长5.5米,当短臂端点下降0.85米时,长臂端点升高多少米?