题目内容
9.在全面奔小康的过程中,家庭轿车的拥有量逐年增加.已知我市某小区2011年底拥有家庭轿车256辆,2013年底家庭轿车400辆.(1)若该小区2011年底到2014年底家庭轿车拥有量的年平均增长率相同,问该小区到2014年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资400万元再建造若干个停车位.据预算,一个停车位的建筑面积为40m2,建造室内停车位2000元/m2、露天停车位200元/m2.根据实际需求,建造露天停车位的数量不少于室内停车位的数量的2.5倍,求该小区最少要再建多少个露天停车位.
分析 (1)设家庭轿车拥有量的年平均增长率为x,根据题意列出方程,求出方程的解即可得到结果;
(2)设该小区要再建x个室内停车位,则露天停车位的数量最少为2.5x,根据投资400万元建立不等式解决问题即可.
解答 解:(1)设家庭轿车拥有量的年平均增长率为x,
根据题意得:256(1+x)2=400,
解得:x1=0.25,x2=-2.25,(不合题意,舍去),
∴400×(1+$\frac{1}{4}$)=500(辆).
答:该小区2014年底家庭轿车拥有量的将达到500辆;
(2)设设该小区要再建x个室内停车位,则露天停车位的数量最少为2.5x,由题意得
2000×40x+200×40×2.5x≤4000000
解得:x≤40,
则2.5x=100.
答:该小区最少要再建100个露天停车位.
点评 此题考查一元二次方程的实际运用,一元一次不等式的实际运用,找出题目蕴含的等量关系于不等关系解决问题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.在△ABC中,∠C=90°,a=5,c=13,用计算器求∠A约等于( )
| A. | 14°38′ | B. | 65°22′ | C. | 67°23′ | D. | 22°37′ |
17.已知△ABC与△A′B′C′的相似比为1:2,△ABC的周长为30cm,并且△A′B′C′的三边比为4:5:6,则△A′B′C′的最长边为( )
| A. | 44cm | B. | 40cm | C. | 36cm | D. | 24cm |
14.如果代数式$\frac{1}{2}{a}^{x}{b}^{y+2}$与-$\frac{1}{3}{a}^{3}b$是同类项,那么x,y的值分别是( )
| A. | x=2,y=3 | B. | x=3,y=-1 | C. | x=2,y=-3 | D. | x=3,y=-2 |
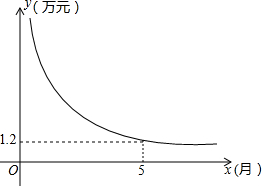 黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.
黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.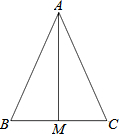 如图所示,在△ABC中,AM垂直平分边BC,若AB=3.6cm,则AC=3.6cm.
如图所示,在△ABC中,AM垂直平分边BC,若AB=3.6cm,则AC=3.6cm.