题目内容
2.已知Rt△ABC的斜边AB=6cm,直角边AC=3cm,以点C为圆心作⊙C.(1)当半径r为$\frac{3\sqrt{3}}{2}$时,直线AB与⊙C相切;
(2)当⊙C与线段AB只有一个公共点时,则半径r的取值范围为r=$\frac{3\sqrt{3}}{2}$或3<r≤3$\sqrt{3}$,
(3)当⊙C与线段AB没有公共点时,则半径r的取值范围为0<r<$\frac{3\sqrt{3}}{2}$或r>3$\sqrt{3}$.
分析 (1)作CD⊥AB于D,如图,根据勾股定理计算出BC=3$\sqrt{3}$,再利用面积法计算出CD=$\frac{3\sqrt{3}}{2}$,则根据直线与圆相切的判定方法得到r=$\frac{3\sqrt{3}}{2}$;
(2)直线与圆相切时,⊙C与线段AB只有一个公共点,则当r=$\frac{3\sqrt{3}}{2}$;当直线与圆相交,且⊙C与线段AB只有一个公共点,则CA<r≤CB;
(3)当直线与圆相离时,0<r<$\frac{3\sqrt{3}}{2}$;当直线与圆相交,且⊙C与线段AB没有公共点,则r>CB.
解答 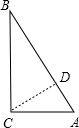 解:(1)作CD⊥AB于D,如图,
解:(1)作CD⊥AB于D,如图,
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴CD=$\frac{3×3\sqrt{3}}{6}$=$\frac{3\sqrt{3}}{2}$,
当r=$\frac{3\sqrt{3}}{2}$时,⊙C与直线AB相切;
(2)当r=$\frac{3\sqrt{3}}{2}$或3<r≤3$\sqrt{3}$时,⊙C与线段AB只有一个公共点;
(3)当0<r<$\frac{3\sqrt{3}}{2}$或>3$\sqrt{3}$时,⊙C与线段AB没有公共点.
故答案为$\frac{3\sqrt{3}}{2}$,r=$\frac{3\sqrt{3}}{2}$或3<r≤3$\sqrt{3}$;0<r<$\frac{3\sqrt{3}}{2}$或r>3$\sqrt{3}$.
点评 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理.

 阅读快车系列答案
阅读快车系列答案| A. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344\end{array}$ | B. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344+306\end{array}$ | ||
| C. | $\left\{\begin{array}{l}13(x+y)=306+344\\ 65(x-y)=344-306\end{array}$ | D. | $\left\{\begin{array}{l}344y=306x\\ 65(x-y)=344+306\end{array}$ |
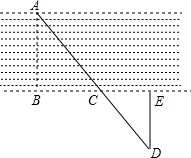 为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )
为了测量一条小河的宽度,小明所在小组同学决定选取河对岸岸边某处为A点,在同侧岸边选取B,C,E三点,使B,C,E在同一直线上,且AB与BE垂直.再过点E作DE⊥BE交AC的延长线于点D,并测得BC=15m,CE=3m,DE=5.4m,则河的宽度AB约为( )| A. | 21m | B. | 24m | C. | 27m | D. | 8.6m |
| A. | 44cm | B. | 40cm | C. | 36cm | D. | 24cm |
| A. | x=2,y=3 | B. | x=3,y=-1 | C. | x=2,y=-3 | D. | x=3,y=-2 |




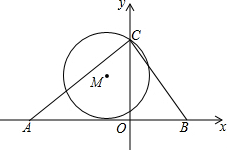 如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).
如图,在△ABC中,AB=10,AC=8,BC=6.点A、B、C都在坐标轴上.⊙M过点C且与x轴相切.设点M(x,y).