题目内容
5．某商店出售某商品时，在进价的基础上加一定的利润，其数量x与售价y的关系如下表所示．请根据表中所提供的信息，列出y与x之间的函数关系式，并求出当数量是2.5千克时的售价．| 数量x（千克） | 1 | 2 | 3 | 4 | … |
| 售价y（元） | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
分析 先根据数量x与售价y如下表所示所提供的信息，列出售价y与数量x的函数关系式y=（8+0.4）x，再将X的值为2.5千克代入上式中即可求出售价．
解答 解：y=（8+0.4）x=8.4x，
当x=2.5千克时，y=8.4×2.5=21（元）．
点评 本题考查了根据实际问题列一次函数关系式，关键找到函数和自变量的关系，用待定系数法求函数的解析式．
练习册系列答案
相关题目
16．在Rt△ABC中，如果各边的长度都扩大2倍，那么锐角A的正弦值与余弦值（ ）
| A． | 都不变 | B． | 都扩大2倍 | C． | 都缩小$\frac{1}{2}$ | D． | 以上都不对 |
13．一列快车长306m，一列慢车长344m，两车相向而行，从相遇到离开需要13s，如果同向而行，快车从追及到超过慢车需要65s，求快车、慢车各自的速度．若设快车速度为x m/s，慢车速度为y m/s，那么，由题意列出的方程为（ ）
| A． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344\end{array}$ | B． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344+306\end{array}$ | ||
| C． | $\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344-306\end{array}$ | D． | $\left\{\begin{array}{l}344y=306x\\ 65（x-y）=344+306\end{array}$ |
10．
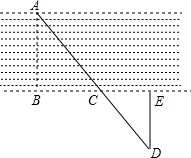为了测量一条小河的宽度，小明所在小组同学决定选取河对岸岸边某处为A点，在同侧岸边选取B，C，E三点，使B，C，E在同一直线上，且AB与BE垂直．再过点E作DE⊥BE交AC的延长线于点D，并测得BC=15m，CE=3m，DE=5.4m，则河的宽度AB约为（ ）
为了测量一条小河的宽度，小明所在小组同学决定选取河对岸岸边某处为A点，在同侧岸边选取B，C，E三点，使B，C，E在同一直线上，且AB与BE垂直．再过点E作DE⊥BE交AC的延长线于点D，并测得BC=15m，CE=3m，DE=5.4m，则河的宽度AB约为（ ）| A． | 21m | B． | 24m | C． | 27m | D． | 8.6m |
17．已知△ABC与△A′B′C′的相似比为1：2，△ABC的周长为30cm，并且△A′B′C′的三边比为4：5：6，则△A′B′C′的最长边为（ ）
| A． | 44cm | B． | 40cm | C． | 36cm | D． | 24cm |
14．如果代数式$\frac{1}{2}{a}^{x}{b}^{y+2}$与-$\frac{1}{3}{a}^{3}b$是同类项，那么x，y的值分别是（ ）
| A． | x=2，y=3 | B． | x=3，y=-1 | C． | x=2，y=-3 | D． | x=3，y=-2 |